はじめてのFRP 靭性評価で扱う エネルギー開放率 とは
今日のはじめてのFRPのコラムでは材料の靭性指標評価にも用いる エネルギー開放率 について考えてみたいと思います。
先週のコラムで紹介した Tencate の TC380 / IM7。
高靭性の材料であり、OHC(開口圧縮)、OHT(開口引張)、
G1C、G2C(それぞれ Mode I、IIのエネルギー開放率、以下、エネルギ開放率)が高い、
ということが紹介されていました。
FRPの材料選定、特に長期の信頼性を担保しようとした時に避けて通れないのが上記の靭性という観点です。
複雑に入り組む結晶粒界に沿って主な亀裂が進展する金属と異なり、
FRPは繊維と樹脂がある程度の規則性を持って整列している構成の材料であり、これが
「破壊の規則性」
という材料の選定と構造設計を困難にする特性を生み出すことになっています。
そのため、トランスバースクラックから始まるFRPの内部破壊は、
ある程度進展した段階で上記の材料構成に応じた規則性を持って急激に進む可能性があり、
しかもその破壊が内部で進展します。
以上のような理由から、FRPにおいては弾性率や強度の高さ、
ということに加え、内部に破壊起点となる初期欠陥や部分的に壊れた場合に、
どれだけ耐えられるのか、粘れるのか
ということを評価します。
これはFRP設計においては定石であり、材料選定の段階から評価することが推奨されます。
そしてこのような材料の破壊や破壊の粘りなどを考える学問を 破壊力学 といいます。
FRPの評価では規格化もされているエネルギ開放率
破壊靭性試験は Mode I、II共に規格化されています。
そのため、試験としては一般的になりつつあるといえます。
Mode I、IIというのは以下のような破壊モードのことをいいます。
本来はMode IIIも見なくてはいけないかもしれませんが、
FRPの世界ではI、II、そしてIとIIの複合モードで評価するのが一般的です。
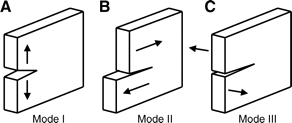
( The image above is referred from http://jeb.biologists.org/content/210/13/2213.figures-only )
そして破壊靭性試験において求めるのが「エネルギ開放率 G」です。
エネルギ開放率は材料(材料構成含む)に固有の物質定数であり、亀裂が進展に対する固体の抵抗度合いを示していると考えても大きな間違いはありません。
このエネルギ開放率。
実はイメージできると非常にわかりやすい指標です。
エネルギ開放率を議論するときにほぼ間違いなく使われる図が以下のものです。
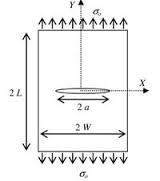
( The image above is referred from http://www.scielo.br/scielo.php?script=sci_arttext&pid=S1679-78252015001102078 )
上図のように内部にある長さ(上図中は2a)の亀裂があるものに、
片側を固定した上である荷重を加える(下に引張る or 上に引張る)と、
荷重点の位置変化による位置エネルギ、亀裂の存在による弾性ひずみエネルギの開放、
そして亀裂の存在による表面エネルギという3種類のエネルギのやり取りが生じます。
亀裂が仮に進展したとする場合、
亀裂進展辺りの位置エネルギの増加と弾性ひずみエネルギの開放量が、
亀裂表面の有する表面エネルギの増加を上回った時に実際の進展が始まる、
というのが大まかな考えです。
参考までにですが上記の評価はASTMの場合、
Mode IがASTM D5528、Mode IIがASTM D7905として規格化されています。
エネルギ開放率の考え方のイメージ
破壊力学の名著、小林 英男 先生の「破壊力学(共立出版)」を参照しながらイメージを書いてみたいと思います。
尚、本図書は以下のURLから購入もできます。
(上記は購入ページにリンク)
出発点として重要なのは弾性ひずみエネルギの考え方です。
以下の図をご覧ください。内部に亀裂を有する試験片に様々な拘束条件や荷重条件を付与した図となっています。
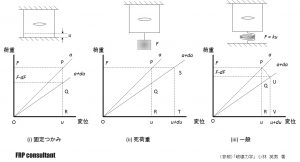
( The image above is licensed by FRP Consultant )
(i)の固定つかみの状態、つまり荷重変位の状態で変位が変化せずに一定であり、
(ii)の死荷重では荷重一定で試験片は自由に伸びている状態です。
この時に三角形OPRで囲まれる面積が弾性ひずみエネルギとなります。
試験片のバネ定数の逆数をコンプライアンスとした場合、
このコンプライアンスは亀裂長さa(上図中のaと対応)の関数となり、
aの増加に伴いコンプライアンスは増加する(バネ定数は減少する)、
つまり剛性が低下するということになります。
ここで実際に亀裂が進展した時の弾性ひずみエネルギの変化について考えてみます。
上図中の(i)の場合、弾性ひずみエネルギは三角形OPRからOQRに減少するため、
弾性ひずみエネルギの減少分三角形OPQの面積が亀裂に与えられるひずみエネルギとなります。
同(ii)の場合、一定荷重Fの条件下で亀裂長さがdaだけ増加した場合、
状態がPからSに変化することで傾きが減少しコンプライアンスが増加します(剛性低下)。
この時は力が一定ですので位置エネルギーにつながる仕事、
つまり四角形RPSTの面積がそれに該当することとなります。
同時に弾性ひずみエネルギが三角形OPRからOSTに増加し、
その差分である三角形OPSが亀裂に与えられた弾性ひずみエネルギとなります。
よって四角形RPSTと三角形OPSの差分が、
力のした仕事と弾性ひずみエネルギの和となり、
面積の関係から結果的に三角形OPSの面積が亀裂に与えられたエネルギとなります。
(底辺をPSと見た時に、三角形OPSの高さは四角形RPSTの長辺STと同じなので、当該三角形の面積は四角形の面積の半分になる)
そして現実を表しているのが上図中(iii)となります。
試験機自体も弾性体ということから試験片との連結間にばねが存在することとなり、
荷重が減少すると同時に同じ力を受けているばねの変位も減少し、
結果として全体の変位を一定に保つように試験片の変位が増大します。
参考までにですが上記のような試験機の有する弾性部分を補正するために、
材料試験を行うにあたってはコンプライアンス補正を行うことがあります。
これは高剛性体を試験機に装着しその時に与えた荷重に対してどのようなS-S線図が引けるのか、
ということで試験機の有するコンプライアンス(つまり、ばね定数)を算出する補正手順です。
当然ながら試験機は設定した荷重では変形しないよう設計されているので、
一般的にコンプライアンスの補正はほとんど必要ないケースが多いですが、
圧縮系試験の場合はコンプライアンス以上に偏荷重がかかっていないのか、
ということに配慮するため、試験片の平面度や垂直度を徹底して検査することが肝要です。
話を元に戻します。
上図(i)、(ii)、(iii)の結果を比較すると、
三角形PSQ、PUQは三角形OPQと比較して微小変化とみなすこともできるため、
三角形OPQとOPSとOPUはほぼ同じ面積とみなすことができます。
つまり、微小長さdaだけ亀裂が進展した時、
亀裂に与えられたエネルギーはいずれのケースもほぼ同じといえます。
上記の考えを踏まえ位置エネルギと弾性ひずみエネルギの変化をコンプライアンスの変化(dC)で表現すると下式のようなシンプルな式になります。
(わかりやすいように位置エネルギと弾性ひずみエネルギは文字で書いていることをご了承ください)
そして上記のGがエネルギ開放率となります。
この式の良いところは固定つかみ、死荷重、試験機が弾性を持っている場合を含め、
すべて網羅できているという汎用性をもっていることです。
そしてこのエネルギ開放率と表面エネルギの増加率(表面エネルギをWとしています)が以下の関係にあるとき、
つまり亀裂の進展によって新たに発生する表面エネルギの増加量よりも、
亀裂に与えられるエネルギ(エネルギ開放率)が大きい場合、
亀裂が進展するということを意味しています。
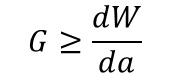
さらにこの表面エネルギは単位面積当たりの量として定義され、γで表示されることが一般的のようです。
亀裂表面の表面エネルギWはγを用いると次式であらわされます。
頭に2がついているのは亀裂の表面は上下あるためです。
![]()
以上のことから亀裂進展に伴う表面エネルギの変化は以下のようにあらわされ、
最終的にエネルギ開放率と表面エネルギの関係は非常にシンプルな関係となります。
下式でいうGcというのが限界エネルギ開放率でCAEでも用いるケースがあります。
![]()
限界エネルギ開放率こそが
「初期から存在する亀裂が進展せずにその材料が耐えられるのか」
を表す指標であり、これを表面エネルギとの比較にすることで材料固有の物理定数と解釈しているのがとても優れた考え方といえます。
式がシンプルなのがいいですね。
やはり優れた理論は式がシンプルというのが特徴ですね。
あくまで対象が弾性体であるという前提はありますが、
少なくとも熱硬化性のFRPについては上記の考えで評価しても大きな懸案はないものと考えます。
いかがでしたでしょうか。
材料の靭性というのが大切である、というのが製品の設計要件に存在するケースもあります。
しかし細かいことは別としても上記のような表面エネルギの増加量と、
弾性ひずみエネルギ、そして位置エネルギの増加量とのバランスで亀裂が進展する、しない、
ということを考えるということが重要といえます。



