はじめてのFRP 界面接着評価 フラグメンテーション法 とは
今日のコラムでは界面接着評価法のひとつである フラグメンテーション法 について書いてみたいと思います。
尚、界面接着法については以前、 プッシュアウト法 についても書きましたので、
ご興味ある方はこちらの記事もご覧ください。
フラグメンテーション法 による評価の理論概要
意外に思われるかもしれませんが、
フラグメンテーション法 の理論の源泉ともいえる、
「 臨界繊維長さ 」
という考えの原点は1960年代の以下の論文から来ています。
Kelly, A. and Tyson, W.R. Tensile properties of fiber-reinforced metals:
copper/tungsten and copper/molybdenum.
Journal of the Mechanics and Physics of Solids, 13, 329-350, 1965
https://www.sciencedirect.com/science/article/pii/0022509665900359
銅をマトリックスとし、タングステンやモリブデンを強化繊維としたときの、
複合材特性を評価した論文です。
Citation Indexは4桁に達しており、非常に評価の高い論文であることがわかります。
近年も引用されるなど、長い時間にわたり様々な研究者の考え方のよりどころになる、
素晴らしい内容なのではないかと考えます。
私もいつかこの論文を読みたい、そして自分の書いた論文も将来そうなってほしいと思っていますが、
とりあえずこの論文で定義されている大切な式をご紹介します。
それが以下の式です。
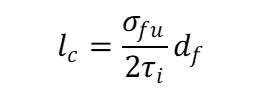
lcが臨界繊維長さ、τiが繊維/マトリックス界面上の任意の位置におけるせん断応力、
σfuが繊維の破断強度、dfが繊維の直径を示しています。
式の意味は極めて明快です。
繊維/マトリックス界面接着せん断強度と繊維の破断強度が釣り合っている、ということを言っています。より具体的には荷重の釣り合いという観点で式を書けばどなたでもわかると思います。
上記のパラメータにおいて、界面接着せん断荷重は、τi*lc*2πdfで、繊維の引張荷重はσfu*πdf2となります。この2つの式が等しいという関係の式を整理すると上記の式になります（πは円周率パイです。）。
この式の示唆することで大切なことは、
「臨界繊維長さは繊維/マトリックス界面せん断強度が高まるほど小さくなる」
ということです。
フラグメンテーション法というのは、この理論に基づいて考えられた試験法であることをまず理解することが大きな一歩になるでしょう。
尚、以下の話は繊維/マトリックスの界面のせん断接着強度は一定であるという仮定にします。
このイメージを持ったうえで、少し進んでみたいと思います。
以下の図を見てください。
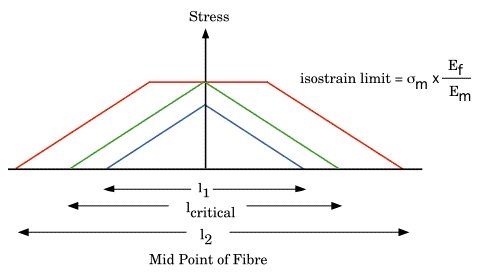
（ The image above is referred from http://www.mse.mtu.edu/~drjohn/my4150/class8/class8.html ）
上図では横軸に繊維長をとり、繊維の中点を原点としています。
縦軸は繊維が担う応力です。
この応力は外力Fが加わったときに発生すると想定してください。
図中の右上の方に「 isolation limit 」と書かれています。
これが「繊維の破断強度」に該当します。
まず、横軸で意味する繊維長の長さに応じて左右から直線的に応力が増加している様子が示されています。
これは、
「応力が一定だとすると、繊維の端部から直線状に応力が増加する」
という仮定の上で成立する線図となります。
尚、上記の話は繊維近傍のマトリックス、及びマトリックスと繊維界面が完全塑性体で破壊しない、
そして繊維とマトリックスが完全に剥離した場合は、荷重が両者の摩擦力によって応力伝達する、
という前提の話です。
マトリックスが弾性体という前提ではありますが、
実際は下図のような応力分布が繊維端面近辺で特異な形状を持つとされています。
※下図は横軸が繊維長で縦軸がひずみとなっています。シミュレーションと実測の比較を行っている図になります。
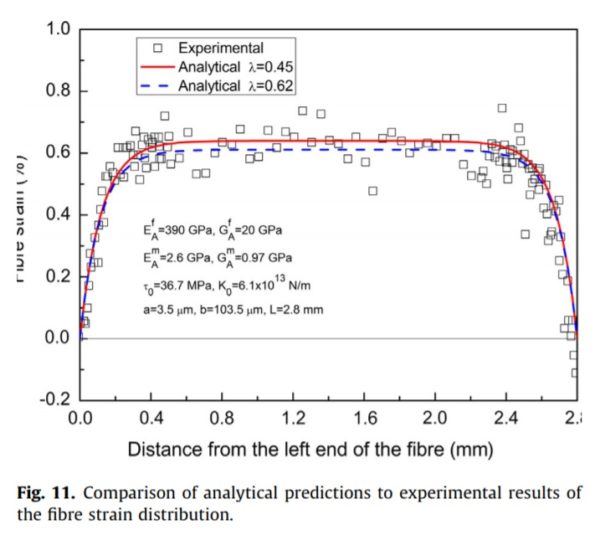
（ The image above is referred from http://users.monash.edu.au/~wyan/papers-pdf/2015/Zuorong-shear-lag-model-mechanics-of-materials-2015.pdf ）
この考えは シェアラグモデル （ shear lag model ）というFRPの業界で、
マトリックスから樹脂への応力伝達の基本理論とされているものです。
シェアラグモデルについては、
上記の「はじめてのFRP 界面接着評価 プッシュアウト法」のコラムでも述べたことがありますので、
そちらをご覧ください。
では実際にこの線図（応力勾配が直線の線図）の意味するものを見ていきます。
繊維長が l1 であるものを見てください。
線図は青い線になっています。
繊維端部から繊維が担う応力は高まっていき、
中点でピークを迎えます。
しかしながらこのピーク値は繊維の破断応力である isolation limit に到達しません。
言い換えると、
「繊維は十分な荷重を担っておらず、外力Fが大きくなっても繊維は破断しない」
ということになるのです。
そのため、外力Fが高まると最終的には
「繊維近傍のマトリックス、または繊維とマトリックスの界面が破壊する」
ということになります。
※ここでいうマトリックスはFRPの場合は樹脂になります。
次に l2 を見てみます。
線図上は赤色で示されています。
上記同様、応力は直線的に高まっていきます。
しかし、l2 は l1 と比べて繊維長が長いため、
外力によって生じた荷重をより多く担います。
そのため、応力勾配に沿って上がってきた応力値が中点（Y軸）に到達する前に isolation limit に到達し、
繊維の破断が生じます。
では、繊維が破断せずに、繊維近傍のマトリックスや、繊維とマトリックスの界面で破壊する最大の繊維長は何か。
その答えが、
「 臨界繊維長さ lc 」
なのです。
上記の線図上では緑色で示されています。
まず、上記のような理論的背景により「 臨界繊維長さ lc」が存在し、
この値がフラグメンテーション法で求める値の理論の根幹にあることをご理解ください。
フラグメンテーション法で求められる繊維/マトリックス界面接着強度
まず理論的背景を踏まえて、
フラグメンテーション法でのせん断強度（繊維/マトリックス界面でのせん断強度）の式を書きます。
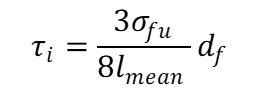
唐突な感じがするかもしれませんが、
上記で述べた界面接着せん断荷重と繊維の引張荷重の釣り合いの式を変形し、lcを4/3倍して、表記をlmeanにしただけです。
では、この式が導き出される背景を説明します。
最初に一つ仮定が出てきます。
この仮定がどのような意味を生じて出てきたのか、
については私自身、もう少し理解が必要であり、元文献を読まなくてはいけませんが、
以下のようなものです。
色々な参考図書にも形を変えて出てきていますが、
結果的な値は同じです。
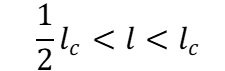
上記の式で示しているのは、
「十分に繊維破断したときの繊維の長さの範囲」
です。
つまり、十分繊維の断片化が進んだ後の繊維長は臨界繊維長さの半分から、
臨界繊維長さそのものの範囲に収まる、ということを言っています。
何故下限値が臨界繊維長さの半分なのかは、
確率論によるものなのか、力学的な検証背景からなのかはわかりませんが、
そういうことのようです。
すると、十分に短くなるまで引張ると、
繊維長の平均値は
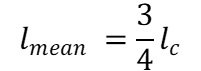
となります。
これは上記の不等式における下限値と上限値の平均を出しています。
この平均値を冒頭紹介した以下の式に導入すると、上記で紹介した
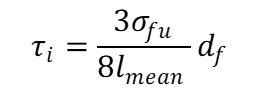
となります。
基本的にはこの式を用いてせん断強度の算出を行います。
とりあえず得られたデータを基本に、上記の式に代入する、という考えはもちろん間違えではありませんが、理論の出所を理解した上で算出できると式の意味合いをより自然に把握できるのではないかと思います。
フラグメンテーション法による試験概要
まず、試験について見ていきましょう。
以下の参考資料をベースに話を進めていきます。
Risø-R-1483(EN)
Testing procedure for the single fiber
fragmentation test
Stefanie Feih, Karen Wonsyld, Daniel Minzari, Peter Westermann, and Hans Lilholt
http://orbit.dtu.dk/files/5223434/ris-r-1483.pdf
デンマークの研究機関の資料であり、とても分かりやすくまとめられています。
以下、項目やFigの番号が出てきますが、これはこの資料中の番号を意味しています。
試験片について
試験片形状については上記資料の 3 Specimen manufacture をご覧ください。
ダンベルに近い形状です。
このダンベルの中に繊維を一本だけ（この場合の一本はストランドやロービングではなく、フィラメントです）入れます。
Fig.5に試験片の外観写真がありますが、
この真ん中に繊維が一本だけ入っています。
この際、繊維の入れ方にもポイントがあります。
繊維にある程度テンションをかけないと、
繊維の真直性が失われることに加え、
マトリックス樹脂の硬化収縮や成形時の残留応力による、
不必要な力がかかるなどのリスクがあります。
加えて繊維の破断前にマトリックスが破壊するというリスクもあります。
これも繊維にある程度テンションをかける必要性につながります。
これについては上記資料中 3.3 Pre-straining the fiber に書かれていますので、
詳細はそちらを参照してください。
試験機器の構成
試験はミクロの視点で評価します。
上記資料 Fig.7 に試験の様子が写真として載っていますが、
ポイントは破壊の状態を顕微鏡で観察しているということです。繊維の直径が数ミクロンから十数ミクロンの世界であることが背景にあります。
実際に観察される画像のイメージは 5.2 Fragmentation length で見ることができます。
試験冶具はFig.6を見ていただくとわかりやすいと思います。小さい枠組みの中に、試験片を引張る機構を備えているのが確認できます。
試験中のひずみは一般的なひずみゲージで求めるケースに加え、
偏光板（ 4.7 Pictures with cross-polarised light ）を用いたやり方もあります。詳細については上記の資料をご覧ください。
試験データと強度の算出
代表的な取得データはFig.14とFig.15で見ることができます。
Fig.14が実際の繊維長の計測の様子、
Fig.15は繊維長の分布を示しています。
繊維/マトリックスの界面接着強度の式は上述した通り、
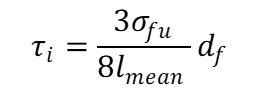となります。
繊維強度はワイブル分布などで求めると上記の引用資料に書かれていますが、
多くは繊維メーカーの値を使うのが実情だと考えます。
結果の解釈
これは参考程度ですが、
上述で紹介した参考資料には、
繊維違い、マトリックス違い、サイジング剤違いといったものの比較も行っています。
繊維とマトリックスの界面せん断接着強度の差により、
破断繊維長分布が右にシフトするが分布勾配に顕著な差異はない（Fig.16）
せん断強度が高いとマトリックス樹脂も同時に破壊される（Fig.17）、
偏光板を用いたひずみ分布では観察面に対して基本的には上下対称であること（Fig.19）、
そのひずみ分布の状態から繊維/マトリックスの界面剥離が生じていることを確認（Fig.20）
といったことが書かれています。
強度だけでなく、このような観点で評価を行うと、
また色々な解釈ができるかと思います。
尚、熱可塑性マトリックス樹脂を用いたフラグメンテーション法の試験片作製を行っている事例もあります。
興味ある方は以下をご覧ください。
http://j-t.o.oo7.jp/lab/t/2009M-yamauchi-ppt.pdf
上記では、マイクロドロップレット法との比較も行っていますね。当該比較において、界面接着強度の相対比較は可能である一方、フラグメンテーション法では残留応力があるため、強度そのものは低めに出ている、という興味深い結果が述べられています。
いかがでしたでしょうか。
今日は、はじめてのFRPのコラムとしてフラグメンテーション法について理論も含め述べてみました。
FRPの界面接着評価は関心が高い一方、
世界的に基準となる確立されたやり方があるわけではありません。
どの手法も一長一短あります。
しかし評価のベースとなる理論を理解し、
再現性のある手順を踏んで準備から試験実施までを推進、
その上で得られた結果を丁寧に検証するという技術の基本が最重要でしょう。
ご参考になれば幸いです。
