「 機械設計 」連載 第三十六回 線形回帰分析である Ordinary Least Square と Total Least Square によるFRP設計許容線図作成とその比較
( The image above is referred from https://pub.nikkan.co.jp/magazines/detail/00001075)
連載開始に関するお知らせについてはこちらをご覧ください。
日刊工業新聞社が発行する月刊誌、「 機械設計 」において
「これからの設計に必須のFRP活用の基礎知識」
という題目での連載の第三十六回目です。
2022年1月号の連載では
線形回帰分析である Ordinary Least Square と Total Least Square によるFRP設計許容線図作成とその比較
という題目で書いています。
2022年1月号は以下のURLから概要をご覧いただけます。
https://pub.nikkan.co.jp/magazines/detail/00001075
FRP動的疲労試験の結果からSN線図(横軸:疲労破壊サイクル数、縦軸:応力振幅)を作成するためには、回帰分析を行う必要があります。回帰分析の分け方の一つとして、非線形と線形があり、アルゴリズムが理解しやすいことから線形回帰分析が望ましいことは過去の連載でも述べています。
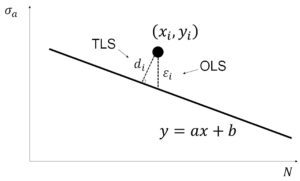
一般的に線形回帰分析というとイメージされるのが最小二乗法。これは Ordinary Least Square (OLS)の一種で、回帰の際は縦軸方向についてのみの分析を行っています。つまり横軸の変動を考慮していないため、回帰分析の精度という観点では課題があるのが実情です。線形回帰分析ながら、どのように回帰分析精度を上げるかという議論の結果として出てきたものの一つが Total Least Square (TLS)です。OLSとTLSの違いは下図を見るとよくわかるかと思います。
(Image above was drawn by FRP Consutant)
当然ながら回帰分析の精度は上がる一方で、TLSの課題は「繰り返し計算が必要である」ということです。
Solverを使いこなせる設計者であれば問題ないが、より汎用的にExcelの一般的な関数でも回帰分析はできないか。
そのような要望に応えられるアルゴリズムの一つが Generalized Minimum Perpendicular Distance Square というものです。
今回の連載では、TLSの一種である Generalized Minimum Perpendicular Distance Square の理論概要を解説した後、当該アルゴリズムを用いた場合とOLSを用いた場合でSN線図の比較を行います。記事の中ではExcelの一般的な関数を用いて、どのように回帰分析を行うのかについても具体的に記述しています。
設計者として最も恐ろしいのは理論の中身がわからずに技術的な業務を進めることです。回帰分析を一例にすると、理論がわからずに複雑なアルゴリズムを適用するよりは、設計者自身が理解できるシンプルなアルゴリズムの方が技術的にははるかに妥当といえます。理論がわかれば、判断の妥当性や限界を理解できるからです。
この次の連載では疲労限度線図の一例としてGoodman線図を取り上げますが、まずその前にSN線図の作成法の理論をきちんと押さえながら、しかしOLSの限界を補完できるTLSを日常業務に取り入れていっていただければと思います。