FRP設計で理解しておきたいせん断応力の対称性/共役性
FRPは異方性が強い材料であるということは、過去の連載で何度も取り上げてきました。
※関連連載
「 機械設計 」連載 第三回 「 異方性 」FRPの最重要特性
「 機械設計 」連載 第十五回 FRP 線膨張率 /異方性の関係と公差設定の留意点
「 機械設計 」連載 第十七回 異方性の理解に向けFRPの 強化繊維配向 を捉える
上記の関連連載でも述べている通りFRPの異方性は他材料に比べて大変顕著である上、
強度や剛性だけでなく線膨張係数にも影響を与える等、
FRPを取り扱う方々にとってFRPの異方性理解は絶対条件とも言えます。
その一方で、FRPの材料が異方性を有しているということを知っていたとしても、
実際に応力解析などをやろうとするとそれを行う方々が別になると、
FRPの異方性をきちんと理解できないまま計算だけ行うというパターンが多いということもあるでしょう。
これはCAEを担当される方が、FRPという材料をよくわかって以内と同時に、
有限要素法の基本を押さえられていないケースもあるのが一因と感じています。
今日は有限要素法の基本に立ち返り、FRPという異方性材料理解の第一歩ともいえるせん断応力の対称性/共役性について考えてみたいと思います。
FRPの理解に絶対不可欠な三次元図
応力の三次元図という言葉を聞いたことはありますでしょうか。
例えば下図のような図がイメージできれば問題ないと思います。
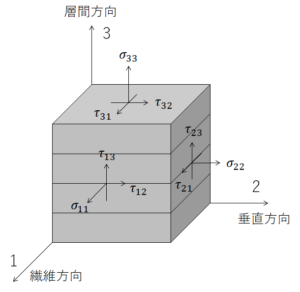
Image above was drawn by FRP Consultant
軸がxyzではなく123となっていますが、これは機械設計の世界でよく用いられる表記法です。
FRPの世界では1軸方向(x軸方向)を繊維方向として表記することが多いです。
そして図中のτ(タウ)がせん断応力です。
せん断応力の対称性/共役性というのは
τ12=τ21
τ23=τ32
τ13=τ31
です。
この関係をご存知な方はいるかと思います。
しかし、どのようにしてこれが算出されるのかというところまできちんといえる方はやや少数派となるかもしれません。
技術の基本を押さえるには、一つひとつ丁寧に考えることが必要ですので、
有限要素法の基本に立ち返ってこの関係を改めて基本から述べてみたいと思います。
微小領域でのモーメントのつり合いで考える
多くの参考図書でもそうですが、3次元だとパラメータが増えるため2次元で考えてみます。
3軸(Z軸)から眺めた12面(XY平面)を想像してみてください。
ここに微小領域(縦dy、横dx)を定義すると、各辺の応力は下図に示すようになります。
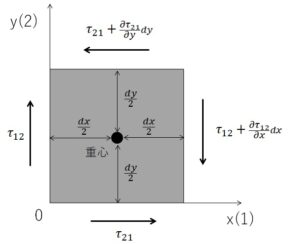
Image above was drawn by FRP Consultant
偏微分があるのは各軸、例えば1軸(X軸)からdx離れたところでは、
応力勾配が生じているためで、その勾配変化分を加算しているとご理解ください。
微小領域の重心を図中の黒丸の通り指定すると、この重心を通る3軸(Z軸)、つまり画面から手前奥行き方向の軸周りのモーメントの”つりあい”を考えると、下式のようになります。
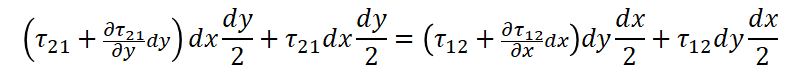
軸の名称が1、2だと微分や偏微分の定義が難しいので、すべてxyに直します。
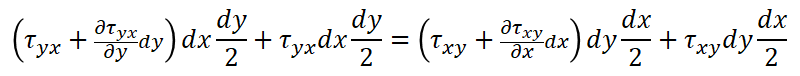
これを展開すると以下のようになります。
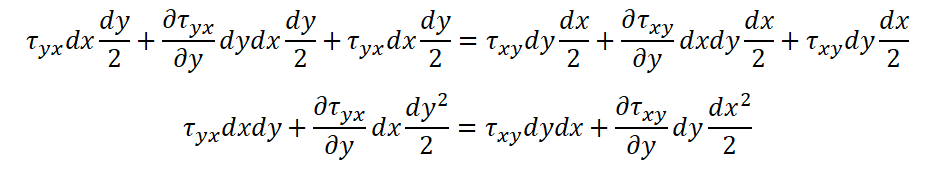
ここで両辺をdxdyで割ると下式になります。
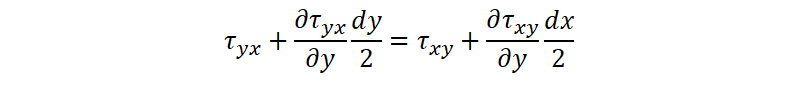
さらに微小領域を0になるよう極限値をとると、
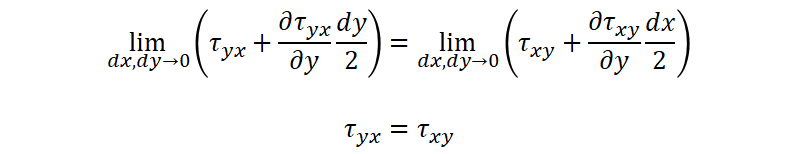
となります。
つまり、軸の名称を1、2に戻すと、
τ21=τ12
です。
これが、冒頭で示した「せん断応力の対称性/共役性」そのものです。
他の軸も同様に計算を行うことができます。
このように、式の一つひとつを丁寧に紐解くという取り組みこそが技術の基本であり、技術者、研究者にとってのグローバル技術言語力とも言えます。
重要なのは理論理解に加え、どう実践するか
感覚的に物事を捉えることを回避する意味も兼ね、
理論的な式も入れながら解説しました。
学術的な意味で言えばこのようなアプローチの繰り返しも一案ですが、
技術として実践するにはこれらをどのように実務に落とし込むのかということを理解する方がはるかに重要です。
材料試験に採用する積層構成設計への好影響
第一に理解すべきは、
「せん断応力の対称性/共役性を応用すれば、評価する試験片の積層構成選択肢が広がる」
ということです。
一例は、FRP破壊の主原因ともいわれる層間せん断の特性値取得です。
この特性値を評価しようとすると、恐ろしく厚めに積層しなくてはいけません。
層間という面外のせん断特性を取るには、厚めの試験片が必要であろうというのは何となく想像できるかと思います。
しかし、
τ13=τ31
ということを知っているだけで、積層構成を変更できることを理解できます。
上記の考えに基づく積層構成の変更によって、積層するFRPの材料Ply数は数倍のスケールで削減可能(数分の1)になります。
詳細は参考図書や試験規格などをみていただければと思いますが、
せん断応力の対称性と共役性を知っているか否かで、
このような考えができるのです。
異方性を加味したCAEへの特性入力値理解
加えてCAEに必要な材料特性を正確に把握することもできるでしょう。
今回ご紹介した有限要素法の基本的な部分の理解は、
そのままCAEの条件設定の理解につながります。
これができるようになれば、様々なシミュレーション精度も高まるでしょう。
加えて異方性を考慮するためには各方向に関する材料物性値が重要であることを理解しているため、どこに注意を払うべきかという危機管理能力向上につながると期待されます。
逆にご紹介したようなせん断応力の対称性/共役性は異方性に気がつかなければ、
CAEを行うにあたって材料特性値の取り扱いに関して疑問を感じることも少ないでしょう。
FRPの破壊形態の主たる面外変形、特に既に述べた層間せん断特性の重要性を感じ取れるか否か、というのも今回ご紹介したような基礎知識の不足が一因といえるかもしれません。
今回ご紹介した内容が、FRPの異方性理解の一助になれば幸いです。



