CFとPEEK、PAEKを組み合わせたFRTP材料間の溶融摩擦に関する研究
近年、適用が拡大している熱可塑性樹脂をマトリックスとしたFRP。
Fiber Reiforced Thermoplasticsを意味するFRTPと呼ばれるこの材料は、
様々な業界でさらなる用途展開が試みられており、
一部は既に実装され始めています。
今回はこのFRTPを使用する際、
積層、成形工程のキーパラメータとなる溶融摩擦に関する研究をご紹介します。
参照元文献
ご紹介する論文は以下のものになります。
本論文はOpen Accessなので、サイトからどなたでも読むことができます。
何故FRTPの溶融摩擦は積層や成形のキーパラメータなのか
本題に入る前にここを理解しておく必要があります。
まず知っておくべきは、
「FRTPは積層がやりにくい」
ことです。
熱可塑性樹脂というのはいわゆる分子鎖が直鎖上に連なった高分子ですが、
身近なプラスチック製品同様、室温だとその表面はさらさらです。
べたつき、いわゆる”タック性”が無いのです。
タック性は材料同士が貼りつくため問題であるという見方もありますが、
別の視点を持たなくてはいけません。
強化繊維が連続繊維のように長い繊維の場合、FRPはシート形状です。
FRPを用いてそれなりの厚みを有する成形体にするには、
シートを重ね合わせる「積層」という工程が必須です。
ここでもしタック性が無いとどうなるでしょうか。
少し触っただけでずれてしまうのがわかると思います。
さらに言えば平面に積層して終わりということはFRP成形体では皆無に近く、
多くの場合で三次元形状にしなくてはいけない。
このような曲率面でタック性のないFRTPは材料を積層位置に固定できないため、
はんだごて等で点付けする必要があります。
しかし、手作業での点付けは大変なので自動積層の出番となります。
Automated Fiber PlacementやAutomated Tape Laying等では積層時に加熱して局所溶融させる
自動積層の代表例がAutomated Fiber Placement(AFP)やAutomated Tape Laying(ATL)です。
どちらもロボットアームなどで、
予め一方向の連続繊維に樹脂を含浸したUD材を規定幅にカットしたテープ材料を、
積層するときだけレーザ等で加熱して溶融させながら積層していきます。
更にこの積層したものに熱と圧力をかけてFRTP間の隙間を無くし、
樹脂を繊維に含浸させる成形が後工程となります。
これらの工程で材料に生じるのが、
「溶融摩擦」
です。
溶融摩擦がどの程度生じるのかを理解することは、
材料の送り速度、押し付け圧力、加熱条件といった積層工程、
並びに成形圧力と成形温度の最適化につながります。
そしてこの溶融摩擦をシミュレーションによって予測できれば、
積層、成形工程の設計精度が高まり、
パラメータをモニタリングできればAI等を通じ、
リアルタイムでの工程の修正も可能となります。
このような背景がFRTPの溶融摩擦理解要望にあることをご理解いただければと思います。
では、早速冒頭で触れた論文の中身について要点を述べたいと思います。
FRTPの溶融摩擦現象を表現するモデルについて
論文中ではFRTPの溶融摩擦を丁寧な前提条件の積み重ねで明らかにしようと試みています。
特に重要な観点について述べたいと思います。
FRTP間をFRTPがすべる際に動摩擦、静摩擦が発生する
溶融摩擦を調べるモデルは
「マトリックス樹脂が溶融状態の際、FRTP間をFRTPがせん断荷重を受けながら滑る」
が基本となっています。
ご存知な方も多いと思いますが、摩擦現象には動摩擦と静摩擦があります。
静摩擦は静止した状態から動き出すまでの摩擦、
動摩擦は一度動き出した後の摩擦を指します。
この現象を連続的な経時変化を表現する非線形線図を用い、
静摩擦の最大荷重をτp、動摩擦の荷重をτ∞として表現しています。
イメージ図は論文中のFig.1をご覧ください。
せん断速度によらず一定の摩擦力を示す過渡期が表れる
この考え方が本論文で大変重要なところになります。
論文中のFig.2に不思議な線図が記載されています。
横軸はShear rateですのでここはせん断速度という理解で大丈夫です。
縦軸はせん断応力であり、FRTP間に生じる摩擦力です。
これを見るとτc,2というせん断応力に到達した際、
せん断速度に応じた摩擦力変化が見られないという現象が、
点線で示されています。
これは私も知らなかった現象です。
論文中ではこれを過渡期(transient)と表現しており、
FRTP間の溶融摩擦理解に重要と位置付けています。
せん断速度向上によって発生する過渡期は繊維界面に存在する高分子鎖の解きほぐしによると想定
この過渡期が生じる理由の一つとして考えているのが、
「繊維界面に存在する高分子鎖の解きほぐし」
です。
熱可塑性樹脂は架橋点を有さない高分子です。
長い分子が絡み合った状態のイメージになります。
三次元架橋をする熱硬化性樹脂と異なり分子の形態変化に柔軟性があり、
上記の過渡期はFRTP中で強化繊維界面付近にいる高分子鎖がほぐれることで生じると考えています。
これを図示したのがFig.3です。
図中赤で示されたのが強化繊維に接触している高分子で、
グレーで示されている壁のようなものが強化繊維である炭素繊維です。
この炭素繊維に接触している高分子鎖は、
強化繊維が図中左右に移動するせん断荷重が発生した際、
接触点を起点として繊維に引張られるイメージとなります。
そうすると層間方向に延びていた高分子鎖が繊維方向に配列し、
繊維がせん断モードで動く際の高分子(熱可塑性樹脂)による抵抗が、
平衡状態になるとのことです。
このような高分子固有の現象が、
Fig.2で示した過渡期発生のメカニズムであると論文中で述べられています。
高分子鎖の解きほぐしは平衡反応と想定
この高分子鎖の解きほぐしは一方向の反応ではなく、
平衡状態であることを想定することが、
実測値と合致させるにあたって重要なようです。
論文中のFig.5に反応図が示されています。
これはFRTPの強化繊維近傍の高分子(熱可塑性樹脂)に関するものです。
Zaは高分子鎖が絡まった状態、
Zdは高分子鎖が解くほぐされた状態、
Zsは解きほぐされた高分子の静的な状態をそれぞれ示しています。
高分子が溶融すれば必然的にZaからZdを経て、
最終的にはZsに収束すると考えられます。
しかしこのモデルでは溶融状態でせん断荷重のかかったすべての高分子が解きほぐされるだけではなく、
その一部はZdからZsに移行せず、再度高分子鎖の絡み合い状態に戻ることを、
反応速度定数を用いて表現しています。
この現象は論文中の式(6)で説明されています。
これを図示化したのがFig.6になります。
時間によって状態が変化する緩和現象が表現できており、
最終的にはZsが優勢となる事がわかります。
更にそれぞれの反応速度定数は、確率論で説明することを試みています。
高分子鎖が絡み合ったZaの状態が優勢なほど、
強化繊維近傍での高分子も分子鎖の動きが抑制される傾向にあり、
それによって繊維と高分子(樹脂)界面では強いせん断応力が発生します。
この事象はどのくらいのFRTP中の高分子が絡み合っているかに依存するため、
Zaの関数として表現できるとの見解が述べられています。
これが論文中の式(7)です。
予測をシンプルにするため、一度ほぐれた高分子が再度絡み合いの状態に戻る反応速度定数と、
ほぐれた状態で落ち着く静的状態に移行する同定数を同じと仮定したのが興味深いです。
高分子である樹脂の特性として絶対に無視できない粘弾性
ここが一般的な材料力学と異なり難しいところなのですが、
樹脂、すなわち高分子は粘弾性という特殊な性質を示します。
粘弾性とは、
「ガラス状態の弾性特性とゴム状態の粘性状態の両方を持ち合わせる」
事を指します。
これを表現しているのが論文中の式(3)です。
剛性を意味するGとせん断応力テンソルτだけでなく、
緩和時間λを考慮した複素関数で示されている、
この虚数iの係数が粘性特性を示す関数です。
緩和現象はゴム成分を有する粘弾性特性だからこそ明確に生じるものと言えます。
論文中ではこの式(3)を1次元の均一なせん断流れとして仮定することで簡略化し、
White-Metzner modelという粘弾性現象を表現するモデルを導入しています。
一言でいえばせん断応力テンソルが面内せん断だけに限定されている式です。
テンソルである必要は無く、面内せん断だけの評価に次元を落としていることになります。
これが論文中の式(4)です。
高分子(樹脂)の粘弾性特性は、面内せん断のみを考慮したこの式(4)で表現されています。
尚、同様のことは変位テンソルDについても行われています。
以下に式を抜粋しました。
上の式がテンソルで表現したもの、下の式が次元を落としたものです。
テンソルは太字で表現されます。
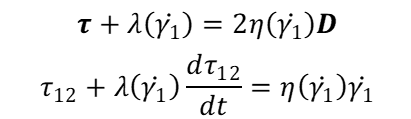
※テンソルについて
「テンソル」というのは方向の固有依存性の事を指し、依存する方向性の数によって階数が示されます。
例えば1階のテンソルといえば一つの方向の依存性を示すもので、4階テンソルは同4つの方向に対する依存を示すことを意味しています。
・引用元の参照コラム
※White-Metzner modelに関する文献例
FRTP間の樹脂層でのせん断現象は樹脂のせん断変形と樹脂の解きほぐし状態に依存する関数で表現
ここまでの想定を取り入れたのがFig.4で示すモデルです。
強化繊維の層間に存在する樹脂自体のせん断変形であるγt、
並びに高分子(樹脂)の解きほぐし状態に依存する関数Vs(t)という、
2つのパラメータで溶融摩擦現象を表現することを示しています。
このVs(t)のVはせん断速度の事を示しており、
式(10)で示す通り反応速度定数との相関関係を定義しています。
FRTPの摩擦実験結果とモデルとの合致性
上述したモデルを用いた溶融摩擦現象の合致性を評価するのに用いたのは、
CF/PEEKとCF/PAEKです。
前者の樹脂はVictrex PEEK 150P、後者は同 AE250Pであるとのこと。
モデルと合致させるには粘度特性が必要であるため、
PEEKは380、390℃、PAEK(Polyaryletherketone)は360、380℃での粘度特性を取得し、
アレニウスプロットによりせん断速度がゼロの際の粘度を算出したと書かれています。
PAEKはPEEKの芳香族ケトン構造(Ph-CO-Ph)がベンゼン環骨格(-Ph-)に置き換わったものです。
構造式は以下になります。
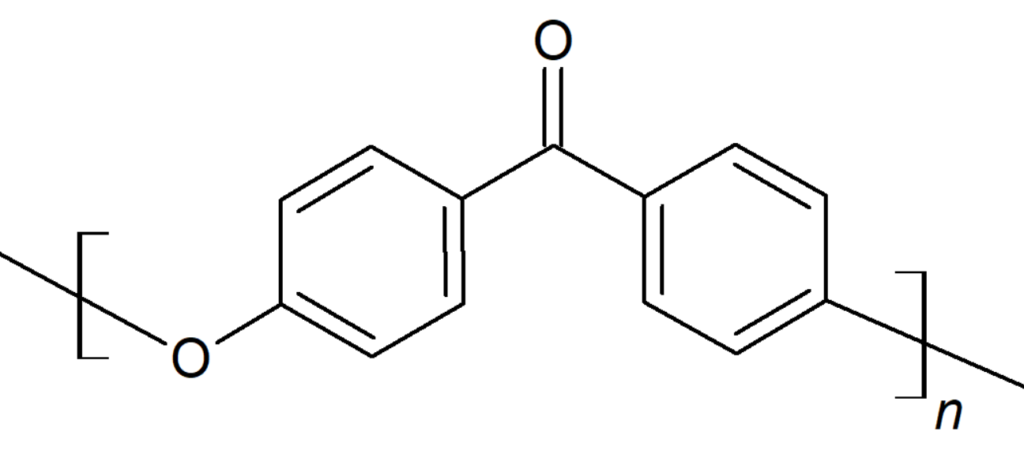
Drawn by FRP Consultant
実測とモデルの比較
それぞれの材料について、縦軸をせん断応力、横軸を変位とした取得した溶融摩擦試験の結果比較を行っています。
実験のやり方詳細は論文5.2項に詳細が述べられていますが、
既述のモデリングにおける前提条件と同じとお考え下さい。
ぞれぞれの材料に関し、3枚の50mm幅のFRTP(UD材)を重ねています。
真中の層の材料だけを250mm長さとし、上下を120mm長さの材料で挟み、
15KPaの圧力をかけながら50mm四方の領域を加熱溶融させた状態で、
真中の材料を引き抜くというものです。
引き抜く速度は5、25、125mm/minの三水準、
加熱温度はPEEK、PAEKでそれぞれ385℃、365℃です。
結果はFig.8に示されています。
モデルによる予想で実測結果を概ね表現できている
色はせん断速度(真ん中の材料を引き抜く速度)の違いを示しており、
実線が実測値、点線がモデルで予測された線図です。
着色領域は計測結果のばらつきの標準偏差を示しています。
全体を通じ、概ね現象をうまくとらえられている印象です。
せん断速度の変化に伴うせん断応力変動傾向も、モデルでうまく表現できています。
実測でPAEKの方がPEEKよりも溶融摩擦が大きいことについても、
モデルで表現できています。
PEEKのせん断応力ピーク値は、125mm/minというせん断速度でずれが生じていますが、
これはモデルでは考慮されていない、マトリックス樹脂中の分子鎖の引抜や破断が起こっているためではないか、
と考察で言及されています。
ただ、個人的にはこのよう機械的な外部荷重で分子鎖の破断はあまり起こらないと考えています。
共有結合はそれほど簡単には切れないと考えるためです。
ソフトウェアへの実装への提案
この論文で興味深かったのは、
モデルを突き詰めて終わりではなく、
シミュレーションを行うソフトウェアに実装することを検討したことです。
予測精度を大きく落とさずに、
計算負荷をどのように下げるかが勝負だといえます。
論文中で述べられた主となる取り組みに触れたいと思います。
反応速度定数を一定にする
結果はFig.11に示されています。
変位が大きいX軸右側に行くほど実測とのずれが生じています。
明確に言及されていないため誤解したかもしれませんが、
ここではFRTP間の樹脂層の厚みを一定として計算したと推測します。
反応速度を一定にし、樹脂層厚みに関する正規化された数値を10セグメントに分ける
このままでは予測精度に難があるということで、
次に取り組んだのが樹脂層厚みに関する正規化された数値を連続的な関数にするのではなく、
セグメントにするということです。
連続的な数値を対象とした計算と比較し、
セグメント化することで計算負荷を大きく下げることになります。
評価点数は約1000程度から10に減るということで100分の1になると書かれています。
このイメージ図がFig.12の(a)です。
この横軸はx/wとなっており、恐らくですが以下の孫文献のFig.7に示された、
繊維の中心軸の位置とその界面の分布から見た樹脂層の厚みの結果を、
正規化したものだと考えられます。
※参照文献
この樹脂層厚みに関する正規化された数値をセグメントとして表現した際の、
せん断応力の実測と予測値の結果がFig.12 (b)に示されており、
計算負荷を下げた状態でもある程度の溶融摩擦発生現象を予測できたと考えられると記載されています。
まとめ
今回はFRTPの溶融摩擦に関する論文をご紹介しました。
熱可塑性樹脂は粘弾性特性とそれに伴う緩和現象が顕著に出ること、
強化繊維付近での高分子鎖の解きほぐしと絡み合いという平衡反応の考慮が必須であること、
そして樹脂層の厚み考慮が溶融摩擦予測精度維持に重要であることをご紹介しました。
今後はせん断速度が連続的に変化する際の溶融摩擦の評価が必要である旨、
論文の中に記載されています。
さらにデータを見る限りPEEKと比べてPAEKの方が分子が、
一度解きほぐされた後の再度の絡み合い現象が起こりやすく、
それが溶融摩擦力向上につながっていること等も明らかになったと考えます。
このことから融点が低いことが、必ずしも溶融粘度低減に直結するとは限らないことになります。
感覚論に依存せず、
このように一つひとつの現象を丁寧に積み重ね、
さらに予測値と実測値の誤差を見ながらモデルの簡略化と最適化を考えることが、
技術的な取り組みとして大変重要であると考えます。
今回ご紹介した論文が、
FRTPを取り扱う際の基礎技術の一端を担う事を期待したいと思います。
※関連コラム



