機械学習のFRPへの適用の現状

技術業界だけでなく、日常にも浸透しつつある人工知能AIは機械学習によって常に情報が更新されています。
有名な対話型AIであるGhatGPTは大規模言語モデルと呼ばれるモデルを基本としており、単語列の生成確率を計算することで自然な言語を生成できると言われています。
※参照情報
今回は人工知能成長と精度向上の基本にある機械学習が、
FRPに対してどのように応用されようとしているのかについてご紹介します。
機械学習とは
技術に関わる者として使用者の目線だけでなく、
どのようなことが中で行われているかの基本は押さえておくべきかと考えています。
私は機械学習の専門家ではありませんが、
概要として知っておいた方がいい技術の基本について調べた範囲で述べたいと思います。
機械学習の大分類である教師の有無
大きく分けて教師有り学習と教師無し学習とありますが、
今回は教師有り学習をベースに述べてみます。
教師無し学習というのは、
明確な答えを与えずに大量の情報を学習させ、
クラスタリングと呼ばれる分類をAIに行わせます。
今回はこちらについては触れないため、もう少し知りたい方は例えば機械学習(教師なし学習)/統計局のページをご参照ください。
それに対して教師有りとは明確な答えが存在し、
機械学習を通じてAIにその答えを精度よく回答できるよう学習させることにあります。
後述するFRPへの応用は教師有り学習が基本となっているため(一部教師無し学習もあり)、
以下は”教師有り学習”をベースに述べたいと思います。
機械学習の流れ
実測データなどを入力し、
その入力データを中間層を経由して重みづけし、
出力されるデータと正解値を比較することで精度を評価する、
ということを繰り返すことで、
「重みづけの最適化を行う」
ことが基本の流れです。
この技術はニューラルネットワークといいますが、
単語は聞いたことのある方が多いかと思います。
ニューラルネットワークは複数層で関連した構成をとるため、
入力データの層を入力層、重みづけを行う層を中間層(または隠れ層)、
出力は出力層と呼ばれるようです。
加えてこの概要の話ではニューラルネットワークは全結合である、
すなわちすべての各層のデータは前後の層のすべてのデータと紐づいていることを前提としています。
中間層では活性化関数による重みづけの試行が行われる
機械学習のポイントは重みづけの最適化にあると述べました。
具体的にどのようなことを行っているのかを数式で示す場合、
入力値X(X1、X2、….Xn)、重みづけのパラメータw(w1、w2…..wn)、
バイアスパラメータをb、活性化関数をh()、出力をuとすると下式のようになります。
a=b+w1X1+w2X2+…..+wnXn
u=h(a)
ここでいうa=の右辺のうち、bを除く部分を”重み付き線形和”といいます。
実際は各層に複数の数値があるので、例えば入力値はX11、X12…X1n、X21、X22…X2m…となり、重みも同様ですが、ここでは簡略化しています。
活性化関数には複数種あり、
ステップ関数、シグモイド関数、正規化線形関数、双曲線正接関数などがあるようです。
活性化関数で重要なのは、
それが重みづけとして価値があるか、それに応じて次の層に数値を送るか否かの判断、
つまりOK/NGのような数値判断を表現できることにあります。
活性化関数の例
シグモイド関数を例にしてみます。
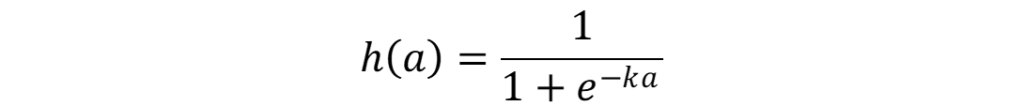
です。eはネイピア数、kはGainです。
この関数の形状はkによって異なる形状を示します。試しにExcelで描写したものを下図に示します。kが大きいほうが勾配が急であり、また極端にkを大きくするとマイナスや1より大きな値を示すことが分かりました。
Gainが大きいとステップ関数の形に近づいていく印象です。
よって活性化関数を最適化するにはGainの調整も重要と考えます。
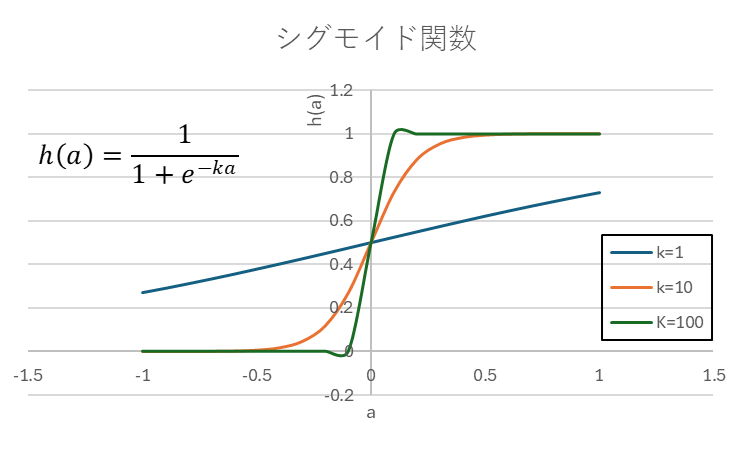
Drawn by FRP Consultant
ただ基本的にはY軸から正の方向に行くほど1に近づき、逆は0に近づきます。
これが数値判断の機能になります。
サイトではステップ関数の形状も示されています。
こちらもOK/NGを示すデジタルシグナルような形状をしているのがわかります。
活性化関数としてもう一つ重要なのが微分できることです。
これは後で少し触れる誤差逆伝播法で活性化関数の微分が必要になるためです。
このようにして活性化関数を導入することで、
線形でしか表現されなかった入力層と重みづけの計算結果である”重み付き線形和”を、
非線形にすることができます。
結果として複雑なパラメータを取り扱うことが可能となる一方、
機械学習の中身がブラックボックスになってしまう一因でもあります。
技術的には課題であると私は考えています。
この辺りは後でまた触れたいと思います。
出力層と正解値の誤差を交差エントロピーで評価
中間層を経て重みづけされた数値のみが、
出力層にたどり着きます。
これらの数値が最終的に行く着く層が出力層です。
出力層と教師データである正解値との比較を行い、
誤差の大小を交差エントロピーで評価します。
交差エントロピーは誤差関数である下式で示されます。

diは教師データ、Yiが出力層の数値です。
ここでいうdiは確率を示しているため、0か1の値を取ります。
正解であれば1、不正解であれば0です。
lnは底がネイピア数eの対数です。
出力層の数値Yi率で示すためソフトマックス関数を用いる
教師データが0か1の確率で示されていることから、
出力層の数値Yiも同範囲の数値で示さなくてはいけません。
その際に用いられるのがソフトマックス関数です。
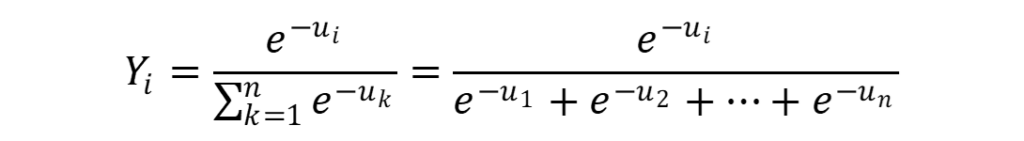
分母が中間層で得られた活性化関数の結果、
既述の通りeはネイピア数です。
分母は得られたすべての活性化関数の結果を指数とするネイピア数のため、
これを分母とすることでYiが確率となり、
こちらは0から1の”範囲”の数字を示します。
誤差関数のイメージをもう少し見ていきます。
誤差関数の評価のイメージ
例えば教師データが不正解の場合、diがゼロになり、正解であれば1です。
出力層の数値はlnYiですのでYiが0から1の値を取るとき負の値となるため(ネイピア数は2.718…で1より大きい)、
誤算関数の最初にマイナスが付いています。
そしてYiが1に近づくほど、lnYiの値は0に近づき、
0に近づくほど負の値の絶対値が大きくなります。
よって、教師データであるdiが大きく(教師有りの場合はdi=1)、かつYiが大きいときに誤差関数Eは小さく、逆の場合に大きくなることがわかります。
これを各出力層についてΣで合算すれば、
教師データとの誤差比較が可能になることがイメージできるのではないでしょうか。
以上のような正解値と誤差関数で示される交差エントロピーの比較を行うことで、
例えば交差エントロピーがいくつ以上になるまで機械学習を継続する、
または同数値が最大値を取るまで重みづけを変えながら、
適切な中間層設定の試行錯誤を行うという機械学習が可能となります。
誤差の最小化に向けた取り組みは誤差逆伝播法が用いられる
なお、この誤差を最小化するためにどのような重みづけの修正が必要なのか、
という検証には”誤差逆伝播法”という手法が使われます。
誤差逆伝播法理解のポイントは、
多変数関数に対する微分公式である”連鎖律”の理解が重要です。
文章が長くなってしまうため誤差逆電波法の詳細内容については、
専門家の解説に譲ろうと思います。
ここからは機械学習のFRPへの適用の現状について述べたいと思います。
機械学習はFRPの業界でも話題の中心になっている
2024年9月9日から始まる北米のCAMXでも機械学習(AI含む)が話題になっています。
例えば、Conferenceだと以下のようなテーマが発表されます。
Smart Manufacturing Leadership: Driving End-to-End Process Improvement
AI-Driven Innovations: Shaping the Future of Materials Development
前者は生産・製造を主としたスマートファクトリーへの取り組みで、
後者は新材料開発業務フロー開発が話題となっているようです。
※関連コラム
CAMX2024 Award Finalistからみる動向
他にもいくつか事例がありますが、産業界でいうと
「材料開発と生産・製造効率化」
が機械学習を経て成長したAIに求められるカテゴリー例と考えます。
以下では機械学習のFRPへの適用について、
論文という形でまとめられたものについて概要をご紹介します。
複合材料モデリングへの機械学習への適用
北米のTEXAS大学が一例です。
取り組みの概要は以下の動画で紹介があります。
動画を見ると考え方の基本はニューラルネットワークであり、冒頭紹介した機械学習と同じ考え方です。
Nonlinear constituteve laws、つまり非線形構成則を学習するとありますが、
こちらも恐らく活性化関数を用いて非線形で評価をする、
ということと大きくは違わないとの理解です。
出力層に直結する実測データがあるものは教師有り学習を行わせ、
そうでない場合は教師無し学習の結果で得られた出力層の値から、
モデルを経由して予測値を算出し、誤算関数の評価を行うという二本立てです。
教師無し学習で評価する内容としては、
非線形の面内せん断挙動、破壊の閾値、損傷の蓄積等が例として挙げられています。
機械学習で重視しているのはモデリングの効率化
機械学習で重視しているのはMultiscale Modelingの生成効率化のようです。
Micro scaleでのモデリングとシミュレーションは複合材料では実用的ではなく、
もう少し俯瞰して全体を把握できるモデルを機械学習を経てAIが作成できないか、
と考えているようです。
Multiscale Modelingによって弾塑性、粘弾性、超弾性、損傷、構造分離といった、
非線形や破壊現象を予測できるのではないかと期待していると考えます。
動画で話をしていたXin (Jeffrey) Liu氏に関連する論文から、
機械学習に関するものを2報ほど抜粋し、概要を述べたいと思います。
損傷した複合材料のモデリング
以下が論文になります。
論文の全体を読めていないため詳細は不明ですが、Positive definite deep neural networks (FE-PDNN) と呼ばれるニューラルネットワークをFEMと連携させ、損傷した複合材料(主としてFRP)の構造応答を予測できるモデリングに向けた機械学習ができた、というのが趣旨のようです。
そもそも損傷を受けた複合材料は挙動が大きく変わってしまうため、
計算を収束させることが難しいとのこと。
それを機械学習を活用しながら、現実に即しながら計算を収束させるための法則をある程度見出したといいたいようです。
一方向材だけでなく、複数配向のFRPに対しても予測ができたとのことで、
動画で述べられていた損傷や構造分離を考慮した複合材料のモデリングというものが、
また一歩近づいたということなのかもしれません。
平織FRPのMultiscale Modelingの実現
こちらも同様に論文を以下に引用します。
動画でも重視していると述べられていた、Multiscale Modelingについてです。
こちらも概要だけ読めましたが、Multiscale Modelingがかなり難しいことを感じます。
まずmechanics of structure genome(MSG)と呼ばれる考え方で、
平織を強化繊維形態としたFRPに対してMicro scaleでの構造解析を行った後、
スケールを上げてMeso scale解析を実施し、
この結果の精度と効率を評価しています。
このモデルを入力層として用いて機械学習をさせ、新しいタイプの代用モデル、これが恐らくMultiscale Modelのことだと思いますが、このモデルを用いて平織FRPの機械特性を向上させるための形状パラメータを調整させます。
結果として得られたモデルは、平織FRPの形状設計最適化に活用できる計算負荷の小さなモデルであると同時に、Micro/Meso scaleの両方の考え方も取り入れられたモデルとなるとのこと。
この考え方は平織に限らず、朱子織や綾織りといった他の織物構成のFRPに対しても応用できるとしています。
”シート形態の2D材料から3D形状”というFRPが最も困難に直面しやすいフェーズで活躍できる考え方といえそうです。
機械学習によるFRP疲労寿命予測
日系自動車メーカの取り組みが一例です。
以下の論文が出されています。
蓄積してきた疲労データを機械学習させ、試験せずに疲労寿命を予想することはできないか、
というのが取り組みの動機にあるようです。
使用しているのは決定木分析
この論文では機械学習の基本として、決定木分析を行っています。
説明変数を設定したうえで目的変数を予測する、
という流れは回帰分析のそれと類似しています。
ただ、決定木分析はOK/NGによる判断が基本です。
ここが機械学習らしい思考工程です。
説明変数に対して直接出力するRandom Forest回帰と、
予測値との誤差を評価しながら誤差が小さくなるよう下層に引き継ぐ、
XGBoost回帰とLight GBM回帰も試行しています。
XGBoost回帰は決定木の”層”が成長していく一方、
Light GBM回帰は最適解に近いと判断した層だけを成長させるというもののようです。
結論では過学習や精度不足があるため、
継続検討が必要と述べられていますが、
丁寧に評価されている印象です。
本論文はデータが多く述べられているため、
別のコラムで取り上げたいと思います。
機械学習のブラックボックス化への対策
ここで一つ述べなくてはいけないのは機械学習というものに対する懸念です。
私個人として最も懸念しているのは、
機械学習の過程が不明瞭であるというブラックボックスのウェイトの大きさです。
「技術判断の背景となったものは何かを数学で説明できるべき」
ということを信念にしている私から見ると、
過程が見えないのは不安でしかありません。
機械学習の結果だけを鵜呑みにするのであれば、
技術を担う人間の存在意義を脅かしかねません。
このような懸念を抱く方々は一定数いるようで、
Local Interpretable Model-agnostic Explanations(LIME)や、
SHapley Additive exPlanations(SHAP)といった、
特徴量の予測結果への寄与を評価するという手法も出てきています。
また既に構築された学習済みモデルに対しても同様の評価が可能なものもあり、
Permutation Importanceは一例のようです。
いずれにしても機械学習を活用したデータの出し入れに溺れず、
試験をはじめとした現物を重視する姿勢を忘れてはいけません。
まとめ
機械学習の概要とFRPへの応用例について述べました。
FRPへの適用でいうとMultiscale modeling、材料開発、生産・製造の効率化、材料寿命予想といった、比較的広範囲への適用が始まっている印象です。
FRPが複雑な材料構成を有する複合材料である故、
もしかすると機械学習はブレークスルーとなるかもしれません。
一方で今回の概要として述べた基礎的な数学理論をはじめ、
背景にある数学を無視して結果だけを見るのは危険でしょう。
こういう時代だからこそ泥臭く、
基本理論をおさえるという技術に真摯な姿勢が求められていると感じます。
※関連コラム
FRP学術業界動向 – FRPの 寿命予想 と破壊形態モデリング研究



