FRP表面へのリブレット形状付与による機能性発現の可能性
FRPの新たな機能化の方向性の一つであるリブレット形状付与について、その可能性について述べたいと思います。

サメ肌はリブレットの一つ
リブレットとは
一言でいうと生物模倣の一種です。
表面を平滑ではなく微小な凹凸にすることで、
主に流体がその表面を流れる際の抵抗を抑制する防ぐ、
といったものが例として挙げられます。
今回はリブレットに関する近年の研究をご紹介したうえで、
FRPへの適用について考えたいと思います。
リブレットに関する研究例
私自身は流体力学について門外漢ですが、
個人的に興味を持った研究を一例としてご紹介したいと思います。
参考にしたのは以下の日本流体力学会で発行されている学会誌内の”境界層の摩擦抵抗低減技術”の特集記事の一つです。
岡林 希依, ミウラ折り型ジグザグリブレットによる摩擦抵抗低減の試み, ながれ. 2021, vol.40, p.264-270
以下、個人的に重要と考えた要点について述べたいと思います。
粘性流体の流れる方向と平行な溝がリブレットの基本構造
近年は様々な形状が提案されているようですが、
粘性流体の流れる方向と”平行な溝の列”がリブレットの基本構造のようです。
1970年代には既に研究が始まったとの紹介もあります。
既に半世紀近い研究の歴史があるということになります。
凹凸形状による表面抵抗低減機能発現のメカニズム
主として2つのメカニズムが重要と記述がされています。
壁近傍のスパン方向の縦渦の揺れの抑制
粘性流体の流れと垂直方向であるスパン方向に、
表面抵抗の原因となる”縦渦”と呼ばれる乱流の再生機構サイクルが妨げられる、
というものです。
結果としてレイノルズ応力と呼ばれる応力が減少するとのこと。
レイノルズ応力は、乱れの変動成分が粘性流体の流れに与える影響を示したもののようです。
レイノルズ数とは
ここで少しだけレイノルズという言葉に関連して、レイノルズ数について触れたいと思います。
※参照情報
レイノルズ数とは乱れなく粘性流体が流れる”層流”という状態と、
乱れた流れである”乱流”の状態のどちらが支配的か、
といったことを示す数値の一種のようです。
なお、層流のような一定の流れになるときは”粘性力”が支配的で、
逆に乱流では”慣性力”が支配的というように考えるのが流体力学の基本とのことです。
動粘性係数をν、代表速度をU、代表長さをLとしたとき、レイノルズ数Reは
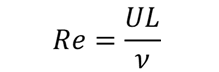
で示されます。
Lは例えば粘性流体が円環の内径部を流れる場合の内径、
Uはその中を通過する粘性流体の速度がそれに該当します。
また、νは粘性係数μと粘性流体の密度ρを用いて下式で示されます。
ν=μ/ρ
よって、νを用いずにReを示すと
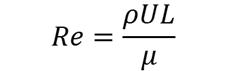
となります。
前出の層流か乱流かを判断する指標として、臨界レイノルズ数というものがあり、
層流状態から乱流状態に急激に変化する閾値として用いられるようです。
※参考情報
レイノルズ数は乱流と層流の状態の比を示す
ρとνで示した前出のReの式の分母と分子にU/Lをかけます。
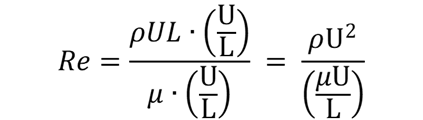
この式の分母が乱流状態を示す指標、分子が層流状態を示す指標とのことです。
これらの意味を理解するためには、
過去にコラムでも紹介したナビエ・ストークス方程式と突き合わせる必要があります。
※過去のコラム
ナビエ・ストークス方程式は下式で示されます。
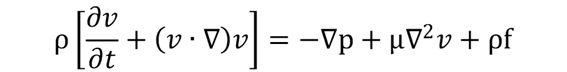
∂(ラウンド)は偏微分、∇(ナブラ)は3つの方向を持った単位ベクトルの偏微分、fは外力です。
この式は流体の”運動方程式”であり、
式内の各項の意味は、左辺から右辺にかけ順番に時間、対流、圧力、粘性、そして外力です。
※参考情報
当該方程式において、乱流状態、すなわち慣性力の指標を示すのは”対流”の項、
同様に層流状態については粘性力について”粘性”の項がそれぞれ該当します。
・対流の項:![]()
・粘性の項:![]()
ここで流速vを代表速度Uで置き換えると、
対流の項はUの二次式、粘性の項はUの一次式であることがわかります。
つまり、
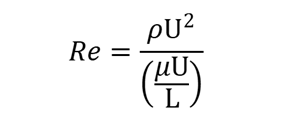
において、Uの二次式である分子が乱流、
Uの一次式である分母が層流の状態に関する度合いを示していると考えることができます。
縦渦によるせん断力を受ける領域の限定
話をリブレットに戻します。
凹凸形状による表面抵抗低減機能発現のもう一つの理由が、
縦渦によるせん断力を受ける領域が、
リブレットの先端に限定されることとのこと。
また渦は溝の中にまで入り込みにくい形状として、
薄いドミノを並べたような形状(Blade riblet)がいい、
という報告もあるようです。
イメージ図は参照記事の図2(b)にあります。
その際、溝の間隔としてs+=15から20という指標も示されています。
なお、s+というのは無次元突起間隔とも呼ばれ、
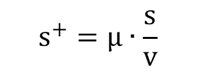
という式で示されるようです。
恐らくμが粘性係数、vが流速、sが突起の間隔だと考えます。
流速や粘性係数が同じ条件であれば、
突起間隔が狭いほどs+は小さくなるものと推測します。
※参照情報
近年は直線状だけでなく曲線やジグザグも登場している
曲線である波状リブレットでは、
従来の直線状のリブレットよりも抵抗低減率が最大2%向上した計算結果がでたとのこと。
波状リブレットは波長と振幅という2つのパラメータで形状が決まるため、
前出のs+と同じロジックで振幅aに対するa+、同様にT(=λ/U)に対するT+を導入し、
ε=a+/T+3
というパラメータで整理した結果、εの値だけで最適化ができる可能性が示されたと述べられています。
ジグザグリブレットは、ジグザグの高さa、波長λ、角度β等のパラメータで、
三角形断面のジグザグリブレットに対してレイノルズ数のみを変えた実験の例も紹介されています。
結果、抵抗低減率は直線リブレットよりも抵抗低減率が劣ったという結果が示された一方、
形状そのものによる断面剛性の向上や、加工のやりやすさ、
溝を薄くできるといった観点も重要であるという、
構造設計や製造の観点からの考察にも触れられています。
形状変化が容易なミウラ折を基本としたジグザグリブレット
リブレット間隔を簡単に変更できる形状で、
かつリブレットに近い構造を持つミウラ折の抵抗低減効果を評価した結果も述べられています。
ジグザグリブレットの波長を三角関数を用いて表現し(参照記事中の式(6))、
非定常な乱流でシミュレーションを行っています。
その結果、リブレットが伸長したときのみ縦渦が多く発生し、
それ以外の形状(収縮時等)ではこの渦の発生が抑制されるという結果が示されています。
理由として渦運動が、伸長運動によって強化された可能性が述べられています。
なお、ミウラ折はポケット地図から宇宙衛星の太陽光パネルまで応用されている、
三浦先生の技術であることはご存じな方も多いかもしれません。
※参照情報
このようにリブレットは流体力学の世界で様々な形状が研究されており、
近年はリブレット形状が可変のものも評価対象になっています。
以下、リブレットのFRPへの適用の可能性について考えてみたいと思います。
FRPに対するリブレットの適用
最初に結論的なことを述べると、
恐らくリブレットをFRPに適用しようという開発はもちろん、
研究もそれほど行われていないのではないか、
というのが私の予想ですが可能性が無いわけではありません。
以下、私見を述べます。
連続繊維強化のFRPにリブレット形状を付与する懸念
通常の平滑面で成形したFRPに後加工でリブレット形状を付与する場合、
加工された箇所の強化繊維の連続性は失われるでしょう。
特に強化繊維が連続繊維の場合、
その影響に注意が必要です。
もちろんFRPは積層構造であるため、
最外層の損傷の構造部材全体への影響に関して金属材料ほど気にする必要はありません。
ただ曲線やジグザグに関わらず、
壁の先端は鋭利な状態になります。
この先端領域は強化繊維が極めて短い状態で存在するにすぎず、
特に熱硬化性樹脂をマトリックスとしたFRPの場合、
ちょっとした力によって面内せん断や層間せん断荷重によって簡単に欠け落ちるでしょう。
私自身はリブレットについて詳しくないので詳細は分かりませんが、
狙った形と異なる時点で表面抵抗が向上してしまう可能性もあり、
何のために当該加工を行ったのかという話になりかねないのです。
FRPという材料構成故、
リブレットで狙った形状を維持できない可能性が、
懸念の筆頭といえます。
金型で転写させるという考え
例えば以下の記事では、FRPを型成形時にリブレット形状を付与するという考えが述べられています。
この記事では金型に凹面形状を付与するとのことです。
Functionalizing surfaces for sustainability / Composites World
本アプローチ自体は悪くありませんが、
こちらもいくつか懸念があります。
以下ではオープンモールドの成形をイメージした見解を示します。
脱型できるか
微小形状とはいえ表面に凹凸をつけるということは、
ミクロ的に見てあらゆるところにアンダーカットができる、
という見方もできます。
そのため、成型するのは良いものの脱型ができないといことも考えられます。
さらにFRPは熱硬化性樹脂を中心に、マトリックス樹脂に接着性の高い有機化合物を用いることが多く、リブレットは強固なアンカー効果を生み出すに違いありません。
金型成型の場合はパーティングラインを複数設ける等、
その設計にかなりの気を使わなくてはいけないと考えます。
※関連コラム
樹脂で埋まる
私個人の経験として真っ先に起こるのはこの事象です。
細かい凹部には樹脂は含浸しないか、
含浸してもそのまま埋まって取れなくなると考えます。
埋まってしまったら、リブレット形状は成形できないのは明らかです。
強化繊維で充填できない
前述の凹部が樹脂で埋まるのは、
その文言の通り樹脂”だけ”が埋まる可能性が高いです。
つまり、強化繊維はそれほど細かいところに流れていかないのです。
連続繊維はもちろんですが、
ガラスマットやランダムマットでも同じでしょう。
オーバーモールディングは可能性がある
確信を得ているわけではありませんが、
熱可塑性マトリックス樹脂をベースとしたFRTPの成形と、
オーバーモールディングを組み合わせれば、
狙いのリブレット形状を有するFRPが得られる可能性があります。
オーバーモールディングは連続繊維をベースとしたFRTPを先に成型し、
その上から射出成型の要領で熱可塑性樹脂、または熱可塑性樹脂+ガラス短繊維で被覆する、
という成形技術です。
可能性のあるものとして過去には腕時計を紹介したことがあります。
※関連コラム
射出成型は短繊維といっても、その長さは長くても数mm以下であり、
機械、物理特性は熱可塑性樹脂単体より高いですが、
概ね熱可塑性樹脂といって間違えではありません。
このような樹脂は型の隅々まで充填できる可能性が高く、
また繊維も短いので強化繊維も到達します。
さらに細かい凹凸形状であっても、
熱可塑性樹脂固有の高い靭性故に壊れにくく、
精密形状を維持しやすいでしょう。
通常のリブレット形状付与は、
フィルムや塗料の加工が主であることを考えれば、
短繊維を含むFRTPでリブレット形状を形成できれば、
耐久性の観点でフィルムや塗料を上回ると期待できます。
※参考情報
大面積リブレット形状塗膜を施した機材を世界で初めて国際線に導入
-世界初、ボーイング787-9型機での燃費改善効果を図る実証実験を開始- / JAXA
AeroSHARK from Lufthansa Technik and BASF now certified for Boeing 777 / BASF
まとめ
これまで何度か述べてきましたが、
今FRPに求められている方向性の一つは”機能化”です。
表面抵抗率を下げるというリブレットを、
FRPに適用するというのはその選択肢の一つになるかもしれません。
空力性能向上の観点で航空機や風力発電向けのFRPにリブレットを適用するという、
今や定石になりつつあるアプローチに加え、
腐食性流体を流す際の配管の内壁にリブレットを適用し、
腐食スピードを低下させることを目的に壁面付近の流速を抑制する、
といった表面抵抗の”向上”を目指すといった考え方も有りうるのではないでしょうか。
機能化を考えるのであれば、
異業種技術の基礎を謙虚に学び、そして協業し、
新しい技術の適用に挑戦するという姿勢が重要だと考えます。



