FRP学術業界動向 – FRPクロス材の 有限要素法 解析
今日は SPE の Composite Devision の定期刊行誌からFRPクロス材プリプレグの 有限要素法 解析に関する技術発表をご紹介します。
表題と作成者の情報は以下の通りです。
題名: End-To-End FE Based Homogenization Of Woven Composites
作成者:
Maxime A. Melchior, Marc Duflot, Jean-Sébastien Gerard, Laurent Adam, Roger Assaker e-Xstream engineering, an MSC Software Company
技術発表内容は以下に抜粋して添付します。
( The paper is referred from the site of "http://www.compositeshelp.com/resources/CompConnMar2015-HighRes.pdf" .)
CAE向けソフトの大手であるMSCからの発表です。
※MSCの情報は以下のHPをご覧ください。
可能な限り見えないものを予想したい、試作で起こるであろう問題をシミュレートしたい。
限られた人数、時間、そしてお金という制約の中で高い質のアウトプットを出すにあたり、CAEの力をかりるというのは間違いのない戦略の一つであると考えます。
今回ご紹介する技術発表は、樹脂をマトリックスとしたFRPクロス材(強化繊維はガラス繊維、炭素繊維)を、Digimat® を用いてFRPのシミュレート最大の難関である、
「繊維とマトリックス樹脂という複数素材構造」
を克服する試みが主な議論内容です。
ベースは繊維と樹脂を均質材として模擬するというもの。
そのアプローチ方法として、
– FE based homogenization
– Mean-field homogenization
という2つのものが紹介されています。
発表資料によると、FE based homogenizationは、
1.強化繊維を均一として模擬
2.ユニットセルを構築
3.代表体積要素( RVE: representative Volume Element )を構築
(RVEについては、https://www.amada-f.or.jp/r_report/kkr/18/12.pdf参照)
4.メッシング
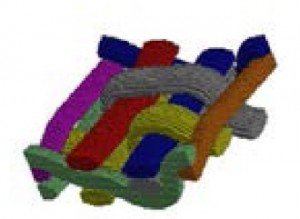
Figure Voxel mesh of woven yarn
( The image above is referred from "http://www.compositeshelp.com/resources/CompConnMar2015-HighRes.pdf".)
5.モデル定義と拘束条件の適用
6.計算実施とそのアウトプット
といった流れとのこと。
編み込まれた繊維をどのように均一化するのか、
代表体積要素でどのようなスケールアップを目指すのか、
といった詳細は述べられていませんが、多くのステップを経て、
「繊維とマトリックス樹脂の複合材料」
を
「異方性を有する模擬均質材」
へと考え方を変化させているのがよくわかります。
その一方で、Mean-field homogenization は Digimat® のコマンドで実施できる均質化技術のようです。
詳細は一切かかれていませんが、以下のようなイメージ図と、
「複数層の材料の基礎的構成要素物性を融合する」
ということによって均質化、つまり homogenization を行っていくと述べています。
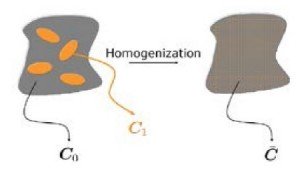
Figure Heterogeneous material (left) from which its equivalent stiffness C is computed from homogenization.
( The image above is referred from "http://www.compositeshelp.com/resources/CompConnMar2015-HighRes.pdf".)
気になる結果を以下に示します。
まずは、均質弾性を想定したガラス繊維/エポキシのFRPについての結果を示します。
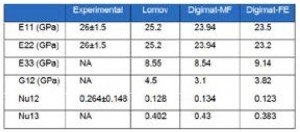
Table: Elastic constants of a balanced plain weave glass/epoxy material: experimental measurements and predictions.
( The image above is referred from "http://www.compositeshelp.com/resources/CompConnMar2015-HighRes.pdf".)
0°方向(warp)の引張強度、弾性率、層間方向の弾性率、面内せん断弾性率とポアソン比、層間せん断のポアソン比などが書かれています。
Digimat MFというのは Mean-field homogenization、Digimat FE というのは FE based homogenizationで均質化された結果を示しています。
個人的な感想としては、かなり精度が高いという印象です。
Digimat MFの層間弾性率に関する実測と差がないことが特に驚きました。
同様に炭素繊維とPPSのFRPに関する結果を以下に示します。
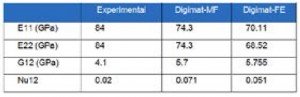
0°方向(warp)の引張強度、弾性率、面内せん断弾性率とポアソン比が書かれています。
Table: Elastic constants of a balanced 5HS T-300 carbon/PPS material: experimental measurements and predictions
GF/epoxyの時と比較し、強度、弾性率、ポアソン比について、均質化手法によらず解析結果と実測の誤差が見られます。
これは予想ですが、上述のガラス/epoxyの時はマトリックス樹脂が熱硬化の剛直高分子だったため、均一弾性体として扱っても問題なかったのですが、PPSのような熱可塑性樹脂だと、破壊に至るまでに早い段階で塑性変形を起こし、弾性体とは異なる振る舞いをした可能性もあります。これがCAEの結果との誤差の一因ではないでしょうか。弾性率をどの程度の低ひずみ領域で判断したのかはわかりませんが、低ひずみ領域に限定した評価であればPPSも弾性体としてふるまうことができ、CAEの結果と近くなる可能性があるのではないかと考えます。
詳細の結果等は本コラム前半に添付したpdfをご覧ください。
さて、このようにして均質化することのメリットは何でしょうか。
メリットの一つは間違いなく、
「計算負荷の低減」
ではないでしょうか。
CAEの中でメッシングというのは最も負荷の高い作業ですが、このメッシングもいくつかの異なる要素を組み合わせるよりは均質材の方がずっと楽に違いありません。
そういう意味では均質化した後で、静的物性でそれなりに近い機械特性と物理特性を予測できたことは一つの重要な確認点かもしれません。
その一方で、Digimat® でFRP構造体の応力解析ができる、と考えるのは時期尚早です。
FRPが3D形状を有する時点でメッシングなどの計算負荷が増大する(ソリッドではなくシェルで計算したとしてもそれなりの負荷ではないでしょうか)のはもちろん、その構造部材の拘束条件を模擬するという難関が立ちはだかるからです。
そして何より、計算「精度」を上げることが大変です。
基本的には実体の応力測定をベースに、CAE側の物理特性や拘束条件を修正していくという地道な作業が要求されます。
この作業の負荷をどれだけ下げられるのかは、解析ソフトを扱う高いスキルを持つ人物、そしてFRPにおいてCAEをどう活用するべきかを広い視点で見ることのできる設計者。
最低でもこの2人(もしかすると、両方できる方もいるかもしれません)が必要です。
CAEを実際に扱われている方やCAE導入を検討されているFRP業界の企業の方のご参考になれば幸いです。