FRP製品の寸法検査における 系統誤差
今日のコラムでは FRP製の製品寸法検査における誤差に着目し、誤差解析の世界でもよく議論される 系統誤差 ( systematic uncertainty )について考えてみたいと思います。
誤差という言葉には ランダム誤差 と 系統誤差 の2成分がある
誤差解析の世界では誤差というと大きく分けて ランダム誤差 と 系統誤差 という2つの考え方があります。
一般的に言われる誤差というのは上記のうちランダム誤差を指すことが多いようです(ほぼ潜在的に)。
ランダム誤差というのはイメージとして繰り返し測定によって明らかになるもの、
系統誤差はそのような繰り返し測定では明らかにできないものを指します。
この系統誤差の厄介なところは、
「取り扱うための理論が存在しない」
ということです。
そのため、経験値をベースとした考え方で、平均値に対してどのくらいの量の誤差が含まれるのか、
という世界のようです。
※参照元:誤差解析入門(東京化学同人)
http://www.tkd-pbl.com/book/b16224.html
結論から先に言うと、FRP製の製品では系統誤差による寸法検査結果への影響が大きいということになります。
FRP製の製品における系統誤差が大きい理由
過去の講演で何度か聴講者向けに行う質問の中に、
「FRP製の製品寸法検査由来の誤差と、製品製造由来の誤差、どちらが大きいと思うか」
というものがあります。
これまでの聴講者の反応だと、6割強が製品製造由来の誤差、いわゆるプロセス由来の誤差とお答えになります。
もちろんプロセス由来の誤差もあります。
ただ、ある程度量を積み重ねてくるとその後差はかなり小さくなる傾向があり、
全体をマクロ的視点で見た時にはほぼ安定したランダム誤差の一部になります。
それと比較し相対的に大きいのが、
「製品寸法検査由来の誤差」
です。
これがすべての製品に当てはまるかわかりませんが、少なくとも私の経験では間違いなくこの傾向があります。
そのため、上記の問いかけに対する私の答えは「寸法検査由来の誤差の方が大きい」となります。
この答えを聞くと中には、
「そのような検査工程は検査の意味をなしていない」
と強く主張される方も居ます。
一般的にはもっともな意見だと思います。
しかしそれはあくまでいくつかの条件(材料が均質材、計測しやすい基準面が広い等)が整ったところでの話になります。
現実は明らかに異なる側面を示すでしょう。
この現実を理解するためにはFRPという材料を理解することが第一歩になります。
FRPは異方性材料である
検査誤差を大きくする主要因、それは
「異方性」
です。
より正確にいうと、
「異方性による、成形後のひずみ」
が誤差としてのってきます。
この誤差が冒頭でご紹介した「系統誤差」となるのです。
FRPは仮にランダム材料であっても必ず異方性が存在します。
そしてこの異方性は一定の方向に積層を行い、
同じ形状で同じ成形加工工程を経ることで常にある方向へのひずみが発生します。
これがFRP製の製品寸法計測の誤差の中で系統誤差を大きくしてしまうのです。
この辺りの話は以下のコラムでも述べたことがありますのでご覧いただければと思います。
FRP戦略コラム – 製品の 寸法管理 に必要な形状設計の考え方
誤差の表現方法はどうすればいいか
ここで少しだけ統計学の話をしたいと思います。
実際の誤差をどのようにして計算するかという実務上の話です。
様々な統計学の確率分布モデルがありますが、
私個人的にはFRPの寸法検査結果を評価するモデルとして「正規分布」が良いのではないかと考えています。
厳密には正規分布では説明できないような結果も出てきますが、
やはり「標準偏差」という考え方が使えるということが実務上でのメリットになります。
実務上では設計、生産、品質保証といった多くのジャンルの異なるメンバー間で、いかに
「イメージしやすい共通言語で評価するか」
ということが重要になります。
その時、正規分布というのは小学生でも習うような最も基本的モデル。
やはりシンプルなモデルをベースに、
しかし実情も考慮しながら評価を進めるというバランスが重要だと考えます。
この辺りの考え方は設計許容値を決める材料データ解析にも共通します。
本点については、以下のコラムでも述べましたのでそちらもご覧ください。
FRPの静的材料データの ばらつき 考慮に向けた統計的考え方
尚、系統誤差を評価する場合、特にN数が少ない場合は
「 母集団標準偏差 」
を用いることをお勧めします。
母集団標準偏差は下式で表されるもので、
一般的な標本標準偏差と比較しルート内の分母が N-1 になっているのが特徴です。
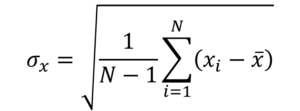
( The image above is drawn by FRP Consultant Corporation/CEO )
標本標準偏差よりも分母が小さいため 母集団標準偏差 の方が大きな値を示す傾向があること、
標本標準偏差では母数の数が小さいときに特に過小評価されがちである、
といったことに考慮がされています。
母集団標準偏差はExcelでも STDEVP という関数で簡単に算出できます。
この辺りは以下のサイトにもう少し書かれていますのでそちらをご参照ください。
http://mh.rgr.jp/memo/ex0022.htm
最後に上記で求められた系統誤差と元々わかっているランダム誤差をそのまま加算して誤差を表現するというアプローチが一般的だと考えます。
もしFRP製品の他の寸法にも汎用的に使いたいということであれば、その確率を正規分布で予想して二乗和を取るというやり方もありますが、FRP製の製品寸法ではこのような一般論は通用しないと私は考えています。
いかがでしたでしょうか。
FRP製の製品寸法検査では系統誤差に対する考慮が必要なことを述べてきました。
結局のところこのような観点を理解するのに重要なのはFRPという材料特性です。
今回のような寸法検査に関する一般的な視野で考えると理解できないのです。
FRPを理解するには幅広い知見が必要であるということについて改めてご理解いただければと思います。



