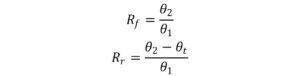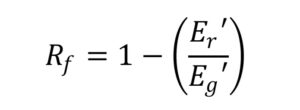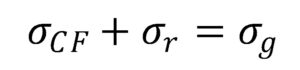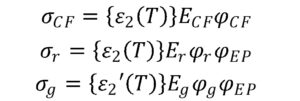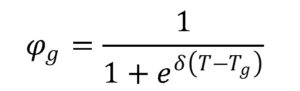FRP学術業界動向 CFRPの 形状記憶特性
今日のコラムでは、日本材料学会の学会誌に掲載されていた、
以下の論文を参考にFRPの 形状記憶特性 ということについて考えてみたいと思います。
炭素繊維/エポキシ樹脂複合材料の形状記憶特性
増谷 勇佑 他
https://www.jstage.jst.go.jp/article/jsms/70/1/70_25/_article/-char/ja/
この文献の切り口は大変興味深いといえます。
構造部材として、いかに剛直にかつ強度を保持するか、
ということが一般的に求められるFRPにおいて、
「一度賦形した形状からどのようにして元の形に戻るのか」
ということを、粘弾性の熱特性を用いながら、その現象の予想を試みるという内容になります。
材料の仕様と作り方
使用したのはCO6343B 100Cという目付198g/sqmの平織クロス材です。
繊維はT300B-3000です。以下を見ると弾性率で230GPa、
強度3530MPaの一般汎用クラスのようです。
https://www.torayca.com/download/pdf/torayca.pdf
マトリックス樹脂はEPIKOTE 828という最も基本的なBis-A型エポキシ樹脂と、
以下に示す4,4′-メチレンビス(シクロヘキシルアミン)を混錬することで100℃、
並びに150℃の温度環境で硬化させたようです。
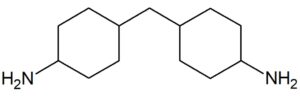
( The chemical structure above was drawn by FRP Consultant )
この樹脂は約160℃のガラス転移温度を示したとのこと。
作り方はエポキシ樹脂を含浸させた0.23mm厚みのクロス材を、
同等の厚みのエポキシ樹脂で挟み込むことで複合材料化したようです。
これを600℃に加熱した残留物(繊維)の重量から、
炭素繊維は25.6wt%だったとのこと。
樹脂の比重が1.4、炭素繊維が同1.76であることから、
Vfになおすと約21.5%くらいですので、
繊維量はそれほど多くありません。
ただ、複合材料を作るという観点だけでいうと、
工夫してうまく作っているのではないでしょうか。
今回の評価では上記のCFRPとマトリックス樹脂単体(Neat Resin)の2種類のサンプルを作製しています。
サイズは長さ40mm、幅が5mmの短冊です。
変形付与と変形量計測方法
変形自体はφ30mmの丸瓶の外側に固定し、
200℃に加熱することで塑性変形を加えた後、
冷蔵庫にて1時間冷却して変形を固定させています。
変形が固定された後、100→200℃への昇温環境に置き、
左右の反りの角度の合成角を変形量として定義しています。
この合成角の変化率を使って形状固定率Rf、形状回復率Rrを求めます。
θの下付が1のものは変形時の変形合成角、同2のものは計上固定時の変形合成角になります。
変形に対する熱挙動はDMAを適用
形状がどのくらい戻るのか、
ということについてはDMA(動的粘弾性測定)を用いています。
動的粘弾性であれば弾性率の変化がリアルタイムでわかるため、
弾性成分(E’)、粘性成分(E”)のバランスがどのように変動するかを把握し、
この変化と実際の試験片形状変化の相関を把握しようという目的があります。
粘弾性については以下のようなコラムでもご紹介したことがありますが、
FRPの材料特性を把握するのには極めて重要な特性の一つといえます。
※ Netzsch が FRP成形加工でも用いる 粘弾性測定 製品を強化
https://www.frp-consultant.com/2020/02/11/netzsch-dynamic-mechanical-analysis/
ここで評価されているのは弾性率がEで示されている通り、引張モードになります。
実測ベースでの形状記憶挙動
樹脂単体とCFRPで、形状記憶状態がどのように変化するかという実測ベースでの結果が述べられています。
冒頭の論文中の図4のグラフがその結果に該当します。
縦軸がRrつまり形状回復率、横軸が温度(100?200℃)になります。
このグラフを見ると、100℃でのRrに差が見られます。
樹脂単体では0.97という初期変形から高い形状復帰特性を示した一方、
CFRPでは0.81となり、形状復帰に向かう変形量が小さいことがわかります。
これは図4で見るとわかるように、100℃という計測開始時点で形状がある程度元に戻ろうとしているため、
初期の変形に伴う合成角が、樹脂単体よりもCFRPが小さいということに由来しています。
この原因は明らかに100℃まで昇温する間において、
炭素繊維の剛性によって形状が元に戻ろうという挙動を示したことにあります。
形状固定率Rfは、G.Liuらが下式によって求められていることを示しており、
今回の樹脂単体とFRPで形状固定率が異なることの説明は理論的にも妥当と考えらます。
※上記式の元文献
Shape Memory of Hydrogen-Bonded Polymer Network/Poly(ethylene glycol) Complexes
Guoqin Liu, Xiaobing Ding, Yiping Cao, Zhaohui Zheng, and Yuxing Peng
Macromolecules 2004, 37, 6, 2228?2232
https://pubs.acs.org/doi/10.1021/ma035717w
図4において、もう一つの注目すべき挙動は、形状回復挙動開始温度です。
樹脂単体ではガラス転移温度付近の160℃弱から形状の回復が始まる一方、
CFRPは140℃弱から形状の回復が始まっています。
これも炭素繊維の剛性が形状回復を助長しているものと考えられます。
論文中では線膨張の影響も検討されていますが、
体積変化は最大でも1%程度でありほぼ無視できると述べられており、
これは私も同感です。
形状記憶高分子複合材料のモデル化
この論文で一番興味深いのはここの部分です。
モデルの考え方がシンプルですが、本質をついているという印象です。
当該モデルのコンセプトは以下のように記載されています。
・炭素繊維は形状回復を担う弾性体
・ガラス状態(低温域)のエポキシ樹脂は炭素繊維による形状回復を阻害する
・ひずみ量は上記2つの力の釣り合いによって決まる
これは私もその通りかと思います。
論文中の図6を見るとわかりやすいです。
引張方向にε1のひずみを与えた状態で冷却し、
そこから加熱を行うことでエポキシ樹脂層に粘性成分、
つまりゴム成分が増加してきた場合、
形状を維持しようとするエポキシガラス成分の応力
= 炭素繊維の弾性成分応力 + ゴム成分の緩和応力
という下式が成り立つことになります。
この場合、各応力は歪みε、体積分率φ、弾性率Eを用いてそれぞれ下式のように示されます。
ε’は圧縮ひずみを示しています。
上記の式を、各モデル上の試験片の長さを用いて表現した後、
ひずみの関係式としてまとめた上で、上記の式を満たす歪みを算出すると、
ε2とε’2の2つのひずみを、弾性率、ひずみ、体積分率だけで表現できるようになります。
(論文中の式8から12までの算出経緯がこれに該当します)
論文中の式に代入する弾性率は、
DMAで実際に計測され、平坦部として示された値を用いたようです。
ガラス転移を落とす前のものをEg、同転移後のものをErとしたとのこと。
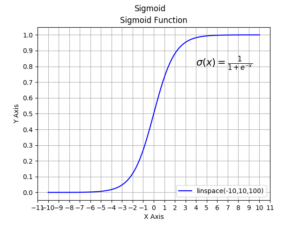
エポキシ樹脂のガラス転移現象は sigmoid 関数を用いています。
sigmoid 関数とは以下のような形の関数になります。
( The image above was referred from https://hackaday.io/page/5331-sigmoid-function )
ガラス転移はいきなり起こるのではなく、
徐々に進行するという状態をうまく表現している関数だと思います。
尚、この関数はAIのアルゴリズムにも用いられている関数とのことです。
そしてモデル上はφg=φr=0.5のところをガラス転移温度としたとのことです。
形状回復率Rrは下式のように歪みで表現できることから、
弾性率とRrの関係をプロット可能となります。
このようにして求められたのが、
論文中図7になります。
状況は良く模擬できていますが、
最大の問題点は、
「弾性率とRrの挙動に合致する炭素繊維量が、実測の方がはるかに大きい」
とのこと。炭素繊維の体積含有率(引張方向に配向しているもの)が0.05%になっただけで、
貯蔵弾性率E’は桁が一つ上がる変化となっていますが、実際には炭素繊維の同含有率が0.18程度にならないと、
同様の数値を示さないとのこと。
この誤差の原因として、以下のようなことが述べられています。
・形状変形に寄与する有効な炭素繊維の量の見積り
・炭素繊維とエポキシ樹脂間の界面接着による変形への影響
ただ、定性的な挙動の予想はできていると書かれています。
また、ガラス転移温度近辺での形状回復率Rrを異なる炭素繊維含有率で比較した結果も示されています。
これは図8になります。
sigmoid 関数の効果もあり、炭素繊維量が多いほど早い段階で形状の回復が発生する、
ということが表現できています。
本研究論文に関して
まず、研究テーマが大変面白いと思います。
FRPを構造部材としてではなく、形状記憶、形状回復という
「機能材としての切り口で評価している」
ということです。
また、モデルをできる限りシンプルにし、
まずは定性的にでも現象を捉えようとする観点は大変興味深いです。
モデルと実測がずれたことについて、筆者の観点については私も同意します。
さらに私個人的に大きな影響を与えていると考えるのが、以下の二点です。
1. 実際の試験は曲げという複合モード、モデルは引張りという単一モード
FRPは異方性のある厄介な材料です。
今回の試験では曲げを行ったことにより、
変形は引張りと圧縮の混合モードになります。
このモードの違いが数値の違いに表れている可能性は疑われるのではないでしょうか。
2. FRPの異方性
加えて考えるべきが上記でも述べた異方性。
特に今回のように曲げで評価してしまうと、
面外変形ですので、細かく言えば大変複雑なモードが発生することになります。
面内せん断はもちろんですが、層間(面外)せん断も起こり、
それに対する弾性率はそれぞれ異なる挙動を示します。
これらの異方性による誤差が、予測と実測の誤差の一員である可能性は否めないでしょう。
異方性については以下のような連載でも述べたことがありますが、
最低でも三次元図をきちんと理解し、
それぞれの方向に対する特性を把握するという姿勢がポイントになります。
※ 機械設計 」連載 第三回 「 異方性 」FRPの最重要特性
いかがでしたでしょうか。
今回の論文は上述の通りFRPを機能性として扱おうとしたことが最も重要です。
さらに、その挙動をできる限りシンプルなモデルで理解しようとするアプローチも重要です。
ここでもお分かりになるように、
熱硬化性樹脂も厳密にいえば高温域でゴム状態となります。
これは高温域では特性が急激に低下するというリスクである一方、
応力集中を回避する、形状追従性が上がるといった別の挙動につながることもあるのです。
熱硬化性樹脂も粘弾性を示すということを改めて認識いただければと思います。
ご参考になれば幸いです。