不織布によるFRPの破壊靭性向上と繊維分散予想へのポアソン分布の応用
熱可塑性樹脂繊維を原料とする不織布を用い、
FRPの重要特性である破壊靭性を向上させよう、
という取り組みについてご紹介します。
また、不織布のFRP層間での分散評価に用いるポアソン分布についても触れます。

破壊靭性はFRPにとって重要な特性
改めて破壊靭性について考えたいと思います。
FRPにおける破壊靭性とは、
内部欠陥を起点とした層間破壊が外部荷重条件で進展するか、
もしくは進展せずに耐えられるのか、
といった”材料の粘り強さ”の指標の一つといえます。
破壊靭性を議論する場合、
通常の構造設計で用いる材料力学ではなく、
破壊力学の考え方を用います。
破壊現象は微小領域で発生するため、
応力集中係数だけでは議論できないためです。
この辺りの詳細は以下のコラムでも述べたことがあります。
※関連コラム
紹介する破壊靭性特性はエネルギー開放率で議論
タイトルにもある不織布による破壊靭性特性の向上に関し、
評価数値はエネルギー開放率を基本としています。
許容損傷サイズを検討するには破壊靭性値が必要ですが、
今回は当該特性の比較を行うという位置づけといえます。
なお、弾性率などの物理定数があれば、
各荷重モードにおいてエネルギー開放率から破壊靭性値を求めることもできます。
上記の話も含めたエネルギー開放率についても、
過去にコラムで取り上げたことがありますので、
この単語をあまりご存じない方はご一読いただければと思います。
※関連コラム
エネルギー開放率の単位換算
最初にエネルギー開放率の単位についてご紹介しておきます。
SI単位をベースとする場合、エネルギー開放率の単位はJ/m2です。
単位面積当たりのエネルギーであり、
イメージしやすいかと思います。
一方で北米を中心に用いられるのがin*lb/in2です。
重さにポンド(lb)、長さにインチ(in)を用いるということです。
つまり比較には単位換算が必要となる場合があるのです。
単位換算はFRPの材料特性を理解するうえで重要になることが多いため、
意味を理解の上、信頼性に難のあるWebサイトでの換算ではなく、
手計算できるようになることをお勧めします。
こういう基本的な部分で効率を求めず、
技術的な理解を深めることは大変重要です。
例えば以下のHexcelのHexPly(R) 3501-6のプリプレグのデータシートをご覧ください。
1ページの真ん中よりやや下にStrain energy release rate, G1cという文字が見えます。
これがMode Iのエネルギー開放率です。
単位がin*lb/in2(またはin*lbf/in2で表記)であることを確認できます。
これをSI単位のJ/m2に換算してみます。
in*lbf/in2→J/m2の換算
Jは1Nの力で1m動かすときに必要なエネルギーで、単位はN*mです。
lbは重さですので、Nを重さになすため、1kgf=9.8N、さらに1kgf=1/0.453lbfの関係を用い、
また1m=1000/25.4inであることから、
1 in*lbf=(1)*0.453*9.8*25.4/1000=0.112761 J
よって、
1 in*lbf/in2=0.112761/((25.4/1000)2)=174.7795 J/m2
になります。
HexPly(R) 3501-6のエネルギー開放率をSI単位に換算
前出の材料について、
エネルギー開放率をSI単位に換算してみましょう。
0.733 in*lbf/in2=0.733*174.7795=128.1134 J/m2
こうすればインチポンド単位の数値をSI単位として、
他の材料と比較することが可能となります。
技術に関わる方は、このように一つひとつのデータの意味を考え、
丁寧に手計算する癖をつけることを推奨します。
このような地道な取り組みの蓄積がいわゆる技術力の基礎となります。
FRPに適用可能な不織布の概要
ここから不織布の話に入ります。
今回参考にしたのは JAMES CROPPER という不織布をはじめとした、
機能性繊維製品を販売する企業が紹介していた以下のサイトになります。
※参照情報
Fracture Toughness / JAMES CROPPER
まずこの製品のポイントについて触れておきます。
材料概要
熱可塑性樹脂繊維として選択可能なのは、
- Polyphenylene sulfide (PPS)
- Polyether imide (PEI)
- Polyester
- Polyether ether ketone (PEEK)
- Polyimide (PI)
です。スーパーエンプラが中心の印象です。
後述する評価結果からはこの使用材料と明確な相関は認められないと述べられているものの、
個人的にはPPSが破壊靭性特性向上に効果的である印象を持っています。
不織布の目付は5から100 g/m2と幅広く、
FRP積層間に適用することでエネルギー開放率が、
Mode Iで最大4.3倍、Mode IIで同3.5倍に上昇すると書かれています。
次にJAMES CROPPERのHP上で不織布の製造メーカであるTECHNICAL FIBRE PRODUCTS INC.が公開していたWebinarから、不織布を用いたFRPの破壊靭性特性評価についてご紹介します。
不織布を用いた破壊靭性値向上への取り組み事例
エネルギー開放率を基軸とした、
不織布のFRPへの層間適用による破壊靭性特性比較についてご紹介します。
<不織布の繊度/目付とエネルギー開放率の関係>
Webinarの元となっている文献は以下のものです。
同じ文献は、筆者がResearch Gateで公開しています。
これに関するTECHNICAL FIBRE PRODUCTS INC.の動画は以下になります。
次に概要を述べます。
評価に使用した材料
Epoxy Araldite(R) LY 564 と Hardener XB 3486を組み合わせたエポキシ樹脂をマトリックスに、
T300の一方向の炭素繊維で強化したFRPです。
ここに繊度(繊維太さ)の異なる不織布、
並びにこれらを組み合わせて目付を高めた不織布を層間に入れ、
エネルギー開放率の評価をしています。
不織布の材料はPPSとPEEKで評価しています。
破壊靭性特性評価法
動画中では縦軸にMode Iのエネルギー開放率G1c、
または同 Mode IIのエネルギー開放率G2c、
横軸がCoverageとなっているグラフが示されています。
このCoverageは被覆率のことで、
断面積あたりの不織布由来の繊維量の多さを意味しているようです。
算出式は元文献の式(3)になります。
よって、基本的には横軸は不織布の目付と読み換えて大きな問題はありません。
不織布の目付に応じて破壊靭性特性は向上するが勾配は一定ではない
まずはG1cから見ていきます。
実際のグラフを見ると目付に応じてエネルギー開放率が右肩上がりとなる一方、
目付が20 g/m2相当の被覆率付近からその上昇が止まり、平坦なデータを示しているのが分かります。
数値をみるとG1cで不織布を用いない300 J/m2程度から、
不織布の目付に応じて800 J/m2に増加しています。
動画の結果では示されていませんが、
文献中ではG2cについても結果が示されており、
類似の傾向がみられるものの、
Mode IIの方がエネルギー開放率の上昇が継続する傾向にあります。
こちらも同様に数値を見ると、
G2cで不織布を用いない1000 J/m2程度から、
不織布の目付に応じて6000 J/m2に増加しています。
このことから不織布を層間に挿入することで、
FRPの破壊靭性特性は向上する一方で、
例えばMode Iでは不織布を多く入れすぎても当該特性が上がり続けるわけではない、
ということが明らかになっています。
単位断面積当たりに存在する不織布由来の繊維量はポアソン分布で予測
前出の”被覆率”の算出において、
FRP断面積中でどのように不織布が分散しているかは、
ポアソン分布で予測していると書かれています。
ポアソン分布とは単位時間あたり平均λ回起こる事象があったとして、
それがk回起こる場合の確率はいくつか、
といった予測をするモデルです。
この分布は下式で示されます。
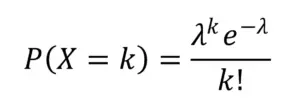
※ポアソン分布の例
例えば1か月当たり平均10個の不良品が出る製造工程があった場合、
同期間内で20個の不良品が出る確率は、下式のように求められます。
P(X=20)=(1020)*e-10/20!=0.001866…
つまり、確率は0.187%程度であると求められます。
この分布は連続ではなく”離散確率分布”であることがポイントで、
離散化しているからこそ、
不連続なFRPの断面中の繊維の分散の表現に応用しやすいようです。
例えば以下のような文献ではセメントを繊維で強化した複合材料において、
繊維分布予想にポアソン分布を用いています。
※参考URL
DFRCC における繊維の分散性評価と 架橋強度のばらつきの検討
ポアソン分布を応用したエネルギー開放率変化の評価
元文献中の式(4)を見てください。
これはポアソン分布の式の中のkに0を代入したものになります。
つまり式(4)は不織布が存在しない領域の存在確率を述べていることになります。
よって、存在しない領域の確率が100%のプロットデータは、
不織布が挿入されていないFRPの値になっています。
同文献中のFigure 14、15の意味は、
不織布が存在しない領域の確率を横軸に、
縦軸にエネルギー開放率をプロットしたものと考えます。
グラフ中の破線は単なるイメージとして記載したとのことであまり意味は有りませんが、
不織布が存在しない領域が少ないほどエネルギー開放率は向上する傾向(左肩上がり)を示し、
特にMode IIでは直線的にエネルギー開放率が上がる結果となっています。
ポアソン分布は二項分布の極限
せっかくですのでポアソン分布にもう少しだけ触れたいと思います。
このポアソン分布はポアソンの極限定理、
いわゆる二項分布の極限で求めることができます。
二項分布は
![]()
であり、ポアソン分布ではnを無限大にします。
ポアソンの極限定理は下式で示されます。
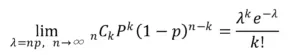
平均値(期待値)を一定にするという制約が重要
ここでのポイントは平均値、
いわゆる期待値を一定にするという考え方です。
前出の通り平均値をλとすると λ=np という関係を常に成立させる、
ということが重要です。
これがぶれるとポアソン分布で評価する際の基準が無くなるためです。
事象を評価する単位時間をn等分し、それを十分に大きく、
つまり細かく分割するとします。
この分割したうえで、その分割区間で起こる起こらない、
言い換えれば0か1の判断をすることは、
まさに二項分布と同等になります。
この理解が、ポアソン分布と二項分布の関係理解につながります。
既に述べた通りポアソン分布の式を求めるには、分割するnを極大化します。
これにより、単位範囲内の分割を無限大にすることで連続事象として捉え、
かつ既に述べた通り平均値が一定、つまりλ=npの関係で左辺が一定の場合、
nを無限大にするとpが小さくなる(λ=npの関係があるため)という制限が発生します。
このようにして単位時間内の事象を確率を念頭に連続的に捉えることが可能となり、
これがポアソン分布の持つ意味と同じになるのです。
FRPの断面に存在する繊維の分布について、
同断面を細かく分けた際、
不織布に該当する繊維が存在する、しないで色分けする、
といった行為をイメージいただくと上記の意味も感じていただけるかもしれません。
最後に今回の結果から考えるべきことについて述べます。
不織布にも異方性がある
動画や元文献において、
エネルギー開放率とCoverageまたは目付の関係を示したグラフを見ると、
MDとCDという記述があります。
これはMDがMachine Direction、CDがCross Directionです。
前者は不織布の長手方向(巻き取り方向)、後者がその垂直方向です。
CDのことはTD(Transverse Direction)ということの方が一般的です。
不織布の弾性率はMDはCD(TD)よりも2倍以上高いという記述があります。
今回のエネルギー開放率評価では、
不織布の異方性に関する明確な影響は認められなかったものの、
一見異方性のなさそうな材料にもその特性があることを認識しておくことは重要です。
FRP破壊で重要なMode IIの破壊靭性を改善させるにあたり不織布は有効な可能性
今回ご紹介した評価において、
Mode Iと比べてMode IIの方が、
挿入する不織布の量と破壊靭性向上の関係において、
不織布の高目付領域に至るまで比較的きれいな比例関係を示しました。
FRPの荷重伝達モードは何度かご紹介した通り、
せん断が主であるというShear lag modelが基本です。
これについては以下のようなコラムでも触れたことがあります。
※関連コラム
Milled Fiber を積層方向に配向させた機能性シート材
試験片をベースにエネルギー開放率を評価する場合、
層間に予亀裂を入れ、
それを開口のMode Iかせん断のMode IIで破壊を進展させます。
Mode Iでは不織布のブリッジであるため、
あまり不織布が多すぎると剛性やマトリックス樹脂による固定が不足し、
結果、破壊しやすくなった可能性があります。
その点、せん断であれば破壊位置に不織布が多くとも、
層間変位が生じないため不織布の粘りが有効に働き、
エネルギー開放率が向上したものと考えます。
試験片のように層間にきれいに破壊が生じるとは限らず、
3D形状だと層間(面外)にも変形が生じることを考えれば、
今回の結果が必ずしも実体評価と同等かはわかりません。
ただ、荷重伝達モードがせん断が主であることを考えれば、
特に面内荷重のみで荷重負荷状況を説明できるアプリケーションであれば、
不織布を多めに入れることで靭性を高めるという考え方そのものは、
有効な材料設計の一案であると感じます。
今回は不織布を用いたFRPの破壊靭性特性評価についてご紹介しました。



